Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 20

2) Случайная величина Х представляет число наступлений события А в n независимых испытаниях, если вероятность р появления события А постоянна в каждом испытании, . (Схема испытаний Бернулли). Закон распределения Х имеет  вид:

;

;

 и т.д. .

Найдем сумму вероятностей: 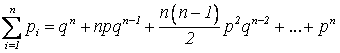 . Справа в равенстве стоит формула «бинома Ньютона» ; тогда 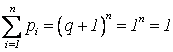, т.к. .

Такая случайная величина Х – число появлений события А в n независимых испытаниях – называется биномиально распределенной.

3) Рассмотрим дискретную случайную величину Х, которая может принимать только целые неотрицательные значения 0; 1; 2; ...; т; ..., причем, последовательность этих значений теоретически не ограничена. Величина Х распределена по закону Пуассона, если вероятность того, что Х примет значение т, выражается формулой:   ,   т = 0, 1, 2, ...;    - параметр закона Пуассона.

Ряд распределения величины Х:

Найдем  .

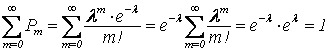Закон Пуассона называется законом редких явлений.

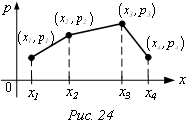Закон распределения случайной величины Х можно изобразить графически в виде ломаной линии, соединяющей точки с координатами (х_i, р_i) в системе координат хОр. Пусть Х имеет закон распределения:

Графическое изображение заданного законом распределения называется многоугольник распределения (или полигон распределения) (рис.24).