Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 10

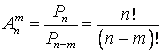
В примере .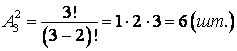

Пример 2  Составить все возможные произведения из трех чисел по два числа (без повтора элементов).

Получим комбинации . Их 3 шт. и они отличаются одна от другой только самими элементами, порядок не важен.

Такие комбинации называются СОЧЕТАНИЯ, обозначаются  и количество всех сочетаний из n элементов по m равно .

Важное свойство сочетаний .

В примере .

3) Правило произведения

Пусть имеем множество элементов  и множество .

Один элемент  можно выбрать k способами элемент у_i Î У можно выбрать т способами. Тогда пару элементов  одновременно можно выбрать способами: каждый х_i сочетается с каждым y_j.

Пример  Из города А в город В можно добраться самолетом и поездом, из В в С – автобусом, поездом и пароходом. Сколько различных возможностей (маршрутов) добраться из города А в город С?

.

6. Основные теоремы теории вероятностей

Определение  Суммой двух событий А + В называется событие С, состоящее в том, что произойдет в испытании хотя бы одно из этих событий – или А, или В, или оба вместе.

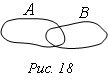
Событие А: материальная точка, брошенная на плоскость, попадает в область А; событие В: точка попадает в область В.       А + В = С – точка попадает или в А, или в В, или в их общую часть.

Сумме А + В соответствует союз «или».

Определение  Произведением событий  Называется событие С, состоящее в том, что в испытании произойдут одновременно и А, и В.

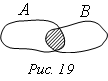Событие  – материальная точка попадет в общую часть (пересечение) областей А и В (и в область А, и в область В одновременно).

Произведению  соответствует союз «и».

Пример  Два стрелка делают по одному выстрелу по мишени.

А: первый стрелок попал в мишень;

В: второй стрелок попал в мишень.

Тогда событие А + В: мишень поражена – попал или первый, или второй, или оба вместе.

Событие АВ: в мишени две пробоины; попали и первый, и второй одновременно.

Определение  События А и В называются несовместными, если они не могут появиться одновременно в одном испытании, т.е. появление одного события исключает появление другого в этом испытании.

Пример  Попадание, промах при одном выстреле.

Определение  Если события А₁, А₂, ..., А_n являются единственно возможными и несовместными попарно в некотором испытании, то они составляют полную группу несовместных событий (ПГНС).

Определение  Два единственно возможных события, образующих ПГНС, называются противоположными.