Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 13

1. Полная группа событий (ПГНС – такая группа А₁, А₂,...,А_n событий, что в результате испытания одно и только одно из этих событий обязательно произойдет; события А₁, А₂, ..., А_n попарно несовместны. Тогда событие А₁ + А₂+...+ А_n – достоверное событие и Р(А₁ + А₂ + ... + А_n) = 1, или, учитывая несовместность событий, имеем Р(А₁ + А₂ + ... + А_n) = Р(А₁) + Р(А₂) + ... + Р(А_n) = 1. Следовательно, сумма вероятностей событий, образующих ПГНС, равна единице,                  т.е. .

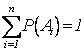2. Противоположные события – два единственно возможных несовместных событий, образующих полную группу. – событие достоверное; . Отсюда,  или .

3. Вероятность осуществления хотя бы одного из независимых событий А₁, А₂, ..., А_n.

Пусть А: произойдет хотя бы одно из А₁, А₂, ..., А_n.

Тогда : не произойдет ни одно из этих событий, т.е. .

Если А₁, А₂, ..., А_n – независимые события, то и события  – тоже независимые. Тогда по теореме умножения имеем:

Следовательно, .

4. Вероятность появления только одного из группы независимых событий А₁, А₂, ..., А_n.

Рассмотрим для простоты случай n = 3.

Пусть А: произойдет только одно из А₁, А₂, А₃, т.е. произойдет или событие , или , или , причем эти события несовместны. Тогда по теореме сложения для несовместных событий имеем:

Аналогично можно вычислить вероятность появления только двух событий из А₁, А₂, А₃: .

Пример:  Студент разыскивает формулу в трех справочниках. Вероятность обнаружить нужную формулу в первом справочнике р₁ = 0,7; во втором р₂ = 0,8; в третьем р₃ = 0,6.

Найти вероятность того, что студент обнаружит формулу 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках; 4) хотя бы в одном справочнике.

1) А: формула есть только в одном справочнике.

2) В: формула есть только в двух справочниках.

3) С: формула есть во всех трех справочниках.

4) D: формула есть хотя бы в одном справочнике.