Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 6

Примеры : 1) , т. М₀(1; 1),  . Найти .

2) , т. М₀(-1; 1);  . Найти .

Метод наименьших квадратов

Табличные задания функции имеем, например, при проведении эксперимента. Наилучший метод получить формулу функции – МНК.

Изложим идею метода, ограничиваясь случаем линейной зависимости двух величин х и у. Сведем результаты n наблюдений  в таблицу

хi	х1	х2	...	хn
уi	y1	у2	...	уn

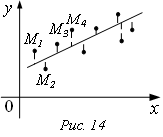
Будем рассматривать х_i и у_i как прямоугольные координаты точек М_i на плоскости, которые группируются вдоль некоторой прямой линии у = ах+b. Считаем в этом случае, что между х и у существует приближенная линейная зависимость.

Рис. 13

Назовем уклонением (отклонением) разность между точным значением функции у = ах_i+b в точке х_i и соответствующим значением у_i из таблицы наблюдений . Отклонения могут быть  или , или .

Будем подбирать параметры а и b в уравнении зависимости так, чтобы искомая прямая проходила как можно ближе ко всем точкам в совокупности. Чтобы исключить влияние знака отклонения, подберем а и b так, чтобы сумма квадратов отклонений была наименьшей, т.е. 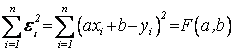 должна быть наименьшей.

 – функция двух переменных, принимает только положительные значения и если она имеет экстремум, то это будет min.

Необходимые условия экстремума:

;  ;  ;  ;

;  ; 

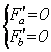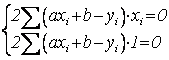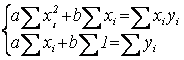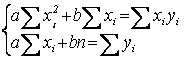
Получили СЛАУ из двух уравнений с двумя неизвестными а, b. Решим ее, например, по правилу Крамера, найдем а, b. Формула зависимости у = ах+ b, полученная по МНК, называется эмпирической (опытной).

Пример : В результате эксперимента получены следующие данные. Найти эмпирическую формулу зависимости

i	xi	yi	xi2	xi yi
1	2	2,2	4	4,4
2	4	4,8	16	19,2
3	3	3,0	9	9,0
4	5	5,1	25	25,5
5	6	5,0	36	30,0
6	1	3,1	1	3,1
7	8	7,0	64	56,0
8	10	11,0	100	110,0
9	7	6,5	49	45,5
10	9	8,4	81	75,6
n=10	S=55	S=56,1	S=385	S=378,3