Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 39

Пример**

4) Огива

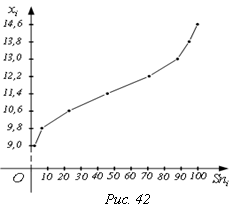По оси ОХ откладываем накопленные частоты Sn_i, по оси ОY – значения вариант x_i. Полученные точки соединяем ломаной линией, график которой называется огива

5) Эмпирическая функция распределения F*(x) – накопленные относительные частоты SW_i

По оси ОХ откладываем варианты x_i, по оси ОY – SW_i . Полученные точки соединяем ломаной линией, график которой называется эмпирическая функция распределения F*(x).

Пример**

xi	9,0	9,8	10,6	11,4	12,2	13,0	13,8	14,6
ni	2	6	15	23	25	17	7	5
Sni	2	8	23	46	71	88	95	100
Swi	0,02	0,08	0,23	0,46	0,71	0,88	0,95	1,0

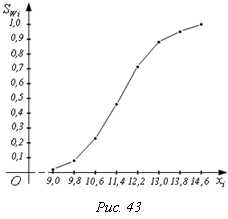
Аналогом F*(x) в т.В является функция распределения F(x) – накопленные вероятности. F*(x) есть оценка теоретической функции распределения F(x) по данным наблюдений.

4. Числовые характеристики варьирующих признаков

4.1 Средние величины обладают способностью характеризовать целую группу однородных единиц одним (средним) числом. Например, средний рост, средняя продуктивность, средняя успеваемость и т.п.

Значение средних заключается в их свойстве аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяет отличать один групповой объект от другого.

Средние величины могут характеризовать только однородную совокупность вариант, в противном случае средняя величина фиктивная.

При вычислении средних величин не обязательно группировать исходные данные в вариационный ряд.

а) Средняя арифметическая   – центр распределения, около которого группируются все варианты статистической совокупности: