Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 47

В примере можно вычислить среднее :

;    ;    ;    .

Аналогично можно найти уравнение регрессии х на у

в виде  .

Корреляционные связи между признаками изучаются только на групповых объектах методами математической статистики.

Корреляционная связь между признаками может быть линейной и нелинейной (криволинейной).

Если изучается зависимость между двумя признаками Х, У, то корреляция называется простой; если между тремя и более – множественной.

Задача корреляционного анализа сводится к установлению направления и формы связи между варьирующими признаками, измерению тесноты связи и к проверке достоверности выборочных показателей связи с использованием соответствующих критериев.

Определение  Эмпирическим коэффициентом корреляции называется величина 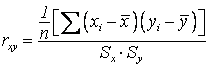 .  . При независимом варьировании признаков Х, У, когда между ними полностью отсутствует связь, r_ху = 0.

Если выборка малая, то удобная формула для расчета , r_ху:

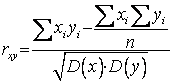,  где   ;    - девиаты.

Пример   Проведены 20 измерений массы Х (кг) мамы-гамадрилы и массы У(кг) новорожденного детеныша. Данные наблюдений сведены в таблицу. Найдем коэффициент корреляции , r_ху