Вопрос №11
Способ построения точки пересечения прямой общего положения с плоскостью общего положения, заданной следами.
Ответ:
Пересечение прямой с плоскостью
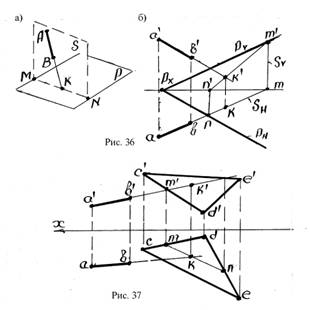
Для определения точки встречи прямой с плоскостью, заданной следами проводится вспомогательная проектирующая плоскость, например, горизонтально-проектирующая плоскость. (плоскость S, рис. 36). Определяется линия пересечения плоскостей (линия mn, см. рис. 36). Определяется точка пересечения фронтальной проекции прямой с линией пересечения плоскостей (точка К, см. рис. 36). Эта точка и является точкой встречи прямой с плоскостью. [3, 4]
Если плоскость задана проекциями треугольника CDE (рис. 37), то также как и в предыдущем примере применяется проектирующая плоскость. Через прямую АВ проводится фронтально-проектирующая плоскость Q. Эта плоскость пересекает стороны треугольника CDE в точках m’, n’ (см. рис.37). Определяются горизонтальные проекции точек и находится точка пересечения линий ab и mn (точка k, см. рис. 37). Эта точка и является точкой встречи прямой АВ с треугольником CDE.
Вопрос № 12
Способ построения линии пересечения поверхностей методом вспомогательных плоскостей, параллельных одной из плоскостей проекций. Привести пример.
Ответ:
Построение линии пересечения поверхностей с помощью плоскостей, параллельных одной из плоскостей проекций
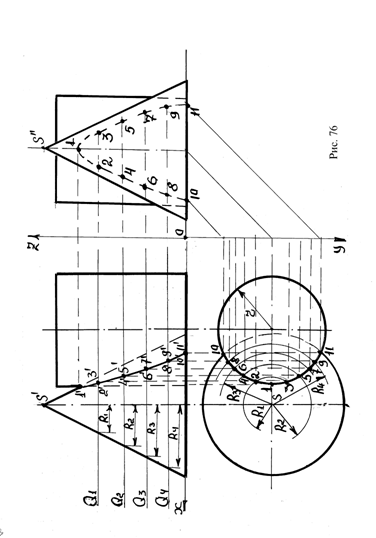
Рассматривается пример построения линии пересечения конуса с цилиндром (рис.76).
В качестве вспомогательных секущих плоскостей выбираются плоскости Q1, Q2 …….Qn ; параллельные плоскости Н. Располагать горизонтальные следы плоскостей целесообразно в промежутке от точки 1’ до основания поверхностей, разделив этот промежуток на П – равных частей.
В рассматриваемом примере выбраны плоскости Q1, Q2, Q3 и Q4.
Плоскость Q1 пересекает конус по окружности с радиусом R1, цилиндр – по окружности с радиусом r , совпадающий с основанием цилиндра.
На горизонтальной проекции строится окружность с радиусом R, и определяются точки пересечения ее с основанием цилиндра – точки 2,3.
Аналогично определяются точки 4,5; 6,7; 8,9; 10,11, представляющие точки пересечения окружности с радиусом R2, R3, R4 с окружностью радиуса r .
Очевидно, точки 2-3 располагаются в плоскости Q1 , поэтому эти точки проецируются на фронтальный след плоскости Q1 – точки 2’ –3’.
Определяются фронтальные проекции точек 4 Ö 11, путем проецирования точек на соответствующие следы плоскостей Q2 .
Находятся профильные проекции точек 1 –11 и по ним строятся линия пересечения поверхностей – профильная проекция.
Фронтальная проекция линии пересечения поверхностей строится по точкам 1’ –11’. Горизонтальная проекция линии пересечения поверхностей совпадает с основанием цилиндра.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.