Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 9

3. Теплопроводность при стационарном режиме

При стационарном режиме температура тела не зависит от времени, т. е.

                                                               .

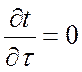Тогда дифференциальное уравнение теплопроводности примет вид:

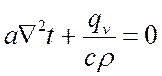                                              , т. к. ,

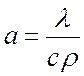или

                                                          .

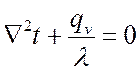Если внутренние источники отсутствуют, то , и тогда:

                                                              ,

или

                                                    .

3.1. Передача тепла через плоскую стенку (без внутренних источников тепла)

3.1.1. Граничные условия первого рода

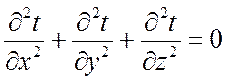Рассмотрим однородную изотропную стенку толщиной d с постоянным коэффициентом l.

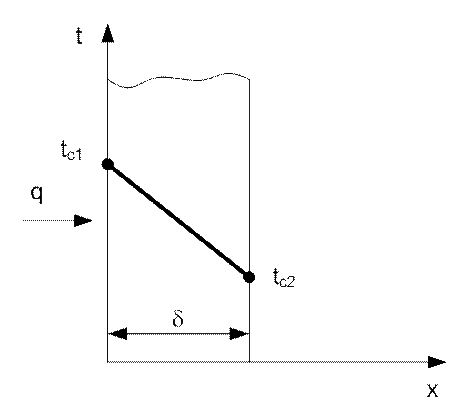
Рис. 7. Теплопроводность через плоскую стенку

Зададим граничные условия:

при x = 0 t = t_с1;

при x = d t = t_с2;

Температура изменяется только в направлении, перпендикулярном плоскости стенки, т. е.

                                                           .

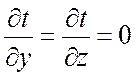Для данного случая уравнение теплопроводности при отсутствии внутренних источников тепла () запишется:

                                                   , или .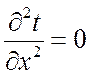

Делаем двойное интегрирование. Первое дает:

                                                              .

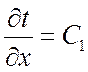Второе дает:

                                                           .                       (*)

Исходя из граничных условий, получим значения постоянных интегрирования C₁ и C₂.

При x = 0 t = t_с1 .

При x = d t = t_с2 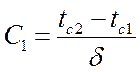 или .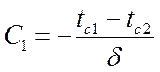

Подставим постоянные интегрирования C₁ и C₂ в уравнение (*). Тогда получим закон распределения температуры в плоской стенке при l = const:

                                                       .

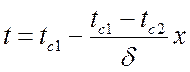Если отсчет избыточной температуры в стенке вести от наименьшей заданной температуры t_c2, то это уравнение можно привести к безразмерному виду. Обозначим:

 – текущий температурный напор;

 – полный температурный напор;

Тогда

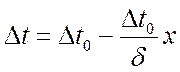                                          , или .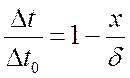

Введя

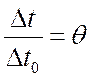 – безразмерный температурный напор,

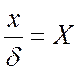 – безразмерная координата,

получим универсальное уравнение:

                                                             .

График изменения температуры представляется единой прямой независимо от t_с1, t_с2 и d.

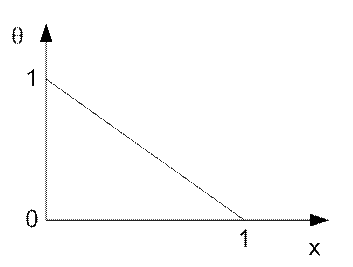
Рис. 8. График изменения безразмерной температуры

Применив закон Фурье 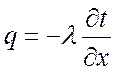 и учтя, что 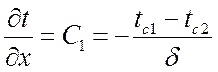, получим плотность теплового потока:

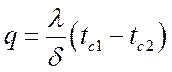                                                  , Вт/м²,

где   , Вт/(м²·K) – называется тепловой проводимостью стенки;

        , (м²·K)/Вт – называется термическим сопротивлением.

Общее количество тепла, переданного через поверхность F стенки за время t:

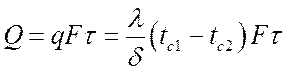                                            , Дж.

Запишем:

                                                           .

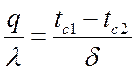Введем это выражение в закон распределения температуры в плоской стенке. Тогда:

                                               .

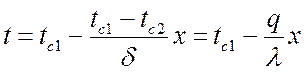Примечание: чтобы найти температуру в каком-либо сечении стенки, необходимо из начальной температуры вычесть отношение удельного теплового потока q к коэффициенту теплопроводности l, умноженному на расстояние до этого сечения.

Распределение температуры в стенке подчиняется закону прямой линии, если рассматривать процесс при l = const.

Однако коэффициент теплопроводности зависит от температуры: . Для многих метало эта зависимость близка к линейной:

                                                         ,

где   l₀ – коэффициент теплопроводности при 0 °C.

На основании закона Фурье:

                                             .

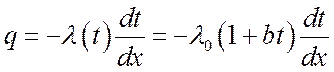Разделим переменные и проинтегрируем в пределах от x = 0 до x = d в интервале температур от t_с1 до t_с2:

                                       ,

                    

,

                                           .

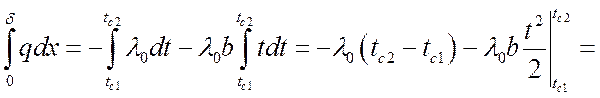
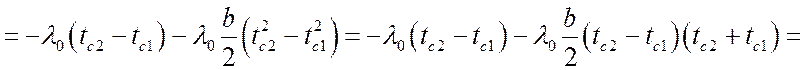
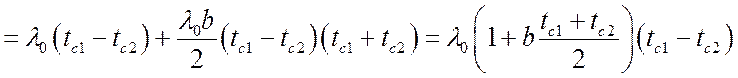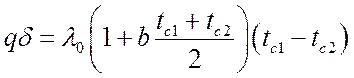Множитель 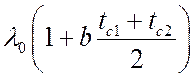 является среднеинтегральным коэффициентом теплопроводности, т. е.

                                                   .

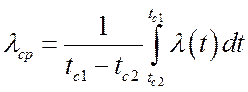Тогда плотность теплового потока на поверхности пластины:

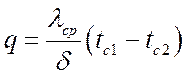                                                 , Вт/м².