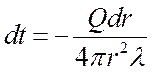Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 15

                                                          .

Интегрируем:

      , ,

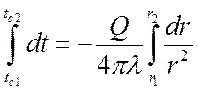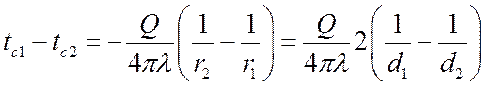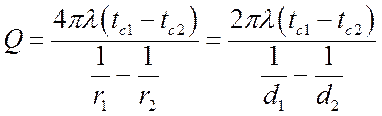                                      , Вт,

                                                     ,

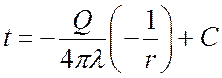где   C – постоянная интегрирования,

                                при  , ,

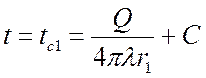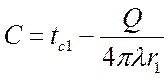                               при  , .

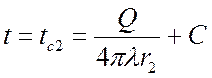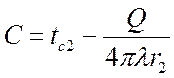Подставляя значения C и Q в уравнение температурного поля, получим:

                                                ,

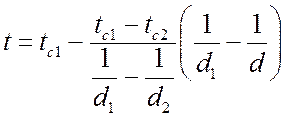где   d – текущее значение диаметра шара.

Из этого выражения следует, что при  температурное поле изменяется по закону гиперболы.

При  уравнение температурного поля примет вид:

                                      .

3.4.2. Граничные условия третьего рода

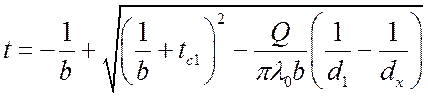Кроме r₁, r₂ задаются t_ж1, t_ж2, a₁, a₂. Полагаем, что t_ж1 и t_ж2 постоянны во времени, а a₁ и a₂ – по поверхности.

Поскольку процесс стационарный, и полный тепловой поток постоянен для всех изотермических поверхностей, то можно записать:

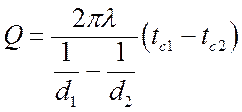                                                 , Вт,

                                                , Вт,

                                                , Вт.

Тогда:

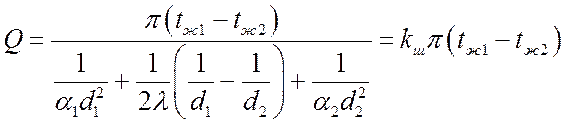                   , Вт,

где 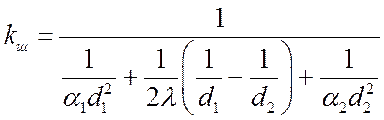  , Вт/K – коэффициент теплопередачи шаровой стенки.

Обратная величина

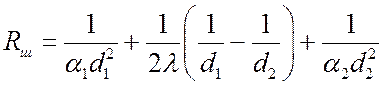                                    , K/Вт

называется термическим сопротивлением теплопередачи шаровой стенки.

3.5. Пути интенсификации теплопередачи

3.5.1. Замечание

Уравнение теплопередачи , Вт, показывает, что количество передаваемого тепла при заданных размерах стенки (F) и температурах сред (t₁ и t₂) зависит от величины k – коэффициента теплопередачи.

Для плоской стенк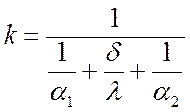и  при 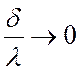 (для тонких стенок с большим коэффициентом теплопроводности l) можно с небольшой погрешностью записать:

                                            .        (*)

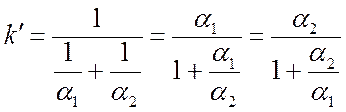Из выражения (*) видно, что k¢ не может быть больше самого малого коэффициента теплоотдачи a₁ или a₂: при  ; при  .

Например:

I       1) a₁ = 40, a₂ = 5000 Вт/(м²·K) ® k¢ = 39,7 Вт/(м²·K);

        2) a₁ = 40, a₂ = 10000 Вт/(м²·K) ® k¢ = 39,8 Вт/(м²·K);

II      1) a₁ = 80, a₂ = 5000 Вт/(м²·K) ® k¢ = 78,8 Вт/(м²·K);

        1) a₁ = 200, a₂ = 5000 Вт/(м²·K) ® k¢ = 192 Вт/(м²·K);

Из примера видно, что при  увеличение большего значения a (в 1 примере) практически не дает увеличения k¢; увеличение же меньшего a в 2 (1 и 3 при одинаковых a₂) и в 5 раз (1 и 4) во столько же раз дает увеличение k¢.

Установлено, что при увеличении a₁ значение k¢ растет быстро до тех пор, пока a₁ не сравняется с a₂. При дальнейшем увеличении a₁ рост k¢ практически прекращается. Таким образом, при  следует повышать то значение a, которое наименьшее, т. е. следует уменьшать большее термическое сопротивление . Если , увеличение k¢ возможно за счет любого из a.

3.5.2. Замечание

Представим термические сопротивления:

цилиндрической стенк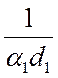и  и ,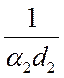

шаровой стенк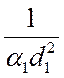и  и ,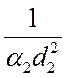

и для плоской оребренной стенки можно записать граничные сопротивления 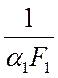 и .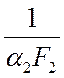

Как видно из этих выражений, термические сопротивления зависят не только от коэффициентов теплоотдачи a, но и от размеров стенки. Увеличение размеров цилиндрической или шаровой стенки (увеличение d) снижает термическое сопротивление. Оребрение плоской стенки при водит к снижению термического сопротивления 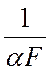 и, следовательно, к интенсификации теплообмена. Причем, если , то оребрять поверхность со стороны a₁ следует до тех пор, пока a₁F₁ не достигнет значения a₂F₂. Дальнейшее увеличение поверхности F₁ малоэффективно.

3.6. Теплопроводность в стержне (ребре) постоянного поперечного сечения

Ребра в технических конструкциях встречаются довольно часто. Ставится задача определить температурные поля в них и тепловые потоки. Причем стержни могут быть самой различной геометрической конфигурации (прямоугольник, круг, треугольник и др. фигуры, в том числе и неправильной формы). Как же решаются задачи теплопроводности в этом случае?

3.6.1. Дифференциальное уравнение и его решение

Рассмотрим простейший случай теплопроводности через ребро с постоянным сечением (прямой стержень).

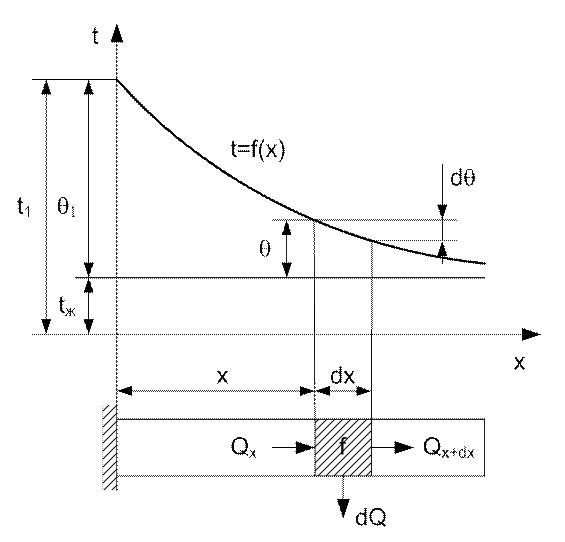
Рис. 20. Теплопроводность в стержне