Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 24

На основании второй теоремы подобия искомая функция в виде безразмерной температуры  в различных сходственных точках 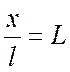 может быть представлена в виде зависимости:

                                                      .

4.2.1. Плоская стенка

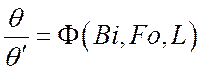Пусть толщина неограниченной плоской стенки составляет 2d (). Если за начало отсчета температуры принять температуру окружающей среды t_ж и обозначить температуру стенки , то для одномерного нестационарного поля можно записать уравнение:

                                                           .

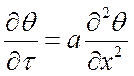Граничные условия:

                                                 при  .

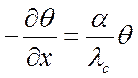Начальные условия:

                                                при  ,

где    – начальная температура стенки при .

Количество тепла, которое может быть отдано плоской стенкой за время полного охлаждения до полного теплового равновесия определим:

                                                         ,

где   F – площадь боковой поверхности пластины.

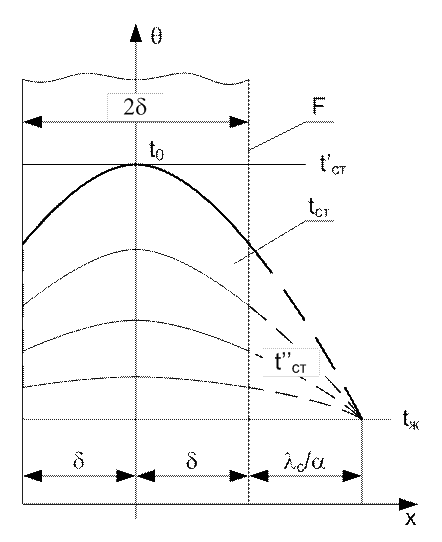
Рис. 36. Нестационарная теплопроводность плоской стенки

В задачах необходимо знать распределение температур на поверхности:

                                                           

и в средней части (слое):

                                                           .

Аргумент L становится постоянным числом (при  , при  ). Следовательно (эти зависимости представлены в [1,2]):

                                                ,

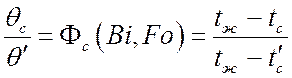где   t_c – текущее значение;

         – начальная температура тела;

                                               ,

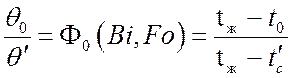где   t₀ – текущее значение;

                                                       .

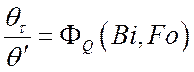а)	б)	в)

Рис. 37.  Зависимость распределения температур от критериев

а) при , ; б) при , ;

а) при Bi = конечная величина, ;

4.2.2. Цилиндр (стержень)

Бесконечно длинный стержень с радиусом R – его дифференциальное уравнение имеет вид:

                                                   .

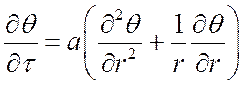Граничное условие:

                                                  при  .

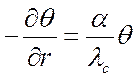Начальное условие:

                                                       при  .

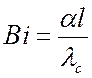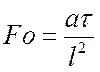Решения ,  и  являются функциями критериев  и . Величина начальной энтальпии:

                                                        ,

где l – длина стержня.

Графики ,  и 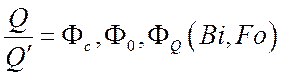 имеют такой же характер.

4.2.3. Шар

Шар радиусом R – для него дифференциальное уравнение имеет вид:

                                                   .

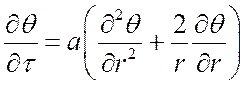Граничное условие:

                                                  при  .

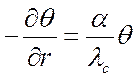Начальное условие:

                                                       при  .

Начальная энтальпия шара

                                                       .

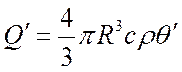Графики имеют аналогичный вид.

4.3. Регулярный тепловой режим

Возьмем твердое тело, охлаждаемое в окружающей среде с температурой t_ж. Условия охлаждения характеризуются коэффициентом теплоотдачи a и остаются постоянными во времени. Внутренние источники тепла в теле отсутствуют.

Примем условие, что разность температур в любой точке тела и окружающей среды имеет один и тот же знак. Весь нестационарный процесс охлаждения (нагревания) тела может быть разделен на две стадии: начальную и стадию регулярного режима.

Первая стадия полностью определяется начальными условиями теплового состояния тела, при этом скорость изменения температуры внутри тела зависит от вида начального распределения температуры. Так, в процессе распределения температуры в пластине безграничной величины

                                              

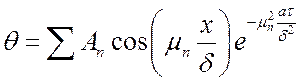
с течением времени t последующие величины ряда будут убывать. Ряд становится быстро сходящимся, и начальная стадия изменения температуры в теле сокращается, начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела и его геометрической формой и размерами.