Тогда:
![]() , Вт/м2.
, Вт/м2.
k – коэффициент теплопередачи. Он характеризует интенсивность передачи тепла от одной жидкости к другой через разделяющую их стенку и численно равен количеству тепла, передаваемого через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один K.
Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи:
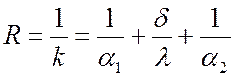 .
.
Оно складывается из частных термических сопротивлений:
![]() .
.
Применив подобные рассуждения для многослойной стенки, состоящей из n слоев, получим полное термическое сопротивление:
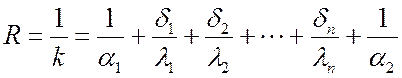 ,
,
или
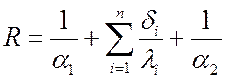 .
.
Отсюда:
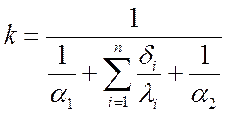 .
.
Тогда:
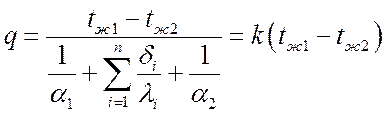 ,
Вт/м2.
,
Вт/м2.
Тепловой поток через стенку, площадь поверхности которой F, будет:
![]() .
.
Температуры поверхностей однородной стенки:
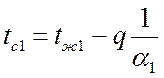 ,
,
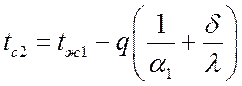 ,
,
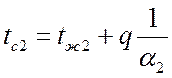 .
.
Для многослойной стенки из n слоев:
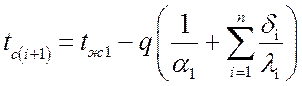 .
.
Для расчета граничных температур применяются и графические методы.
В основу одного из них положено свойство линейной зависимости температурного напора в системе от термического сопротивления, т. е.
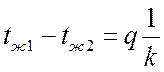 ,
,
для любого слоя:
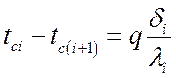 .
.
Это дает возможность построить фиктивную стенку, в которой
толщины слоев будут пропорциональны соответствующим термическим сопротивлениям,
а внешние термические сопротивления теплоотдачи ![]() и
и ![]() учитываются введением двух условных
граничных слоев соответствующей толщины.
учитываются введением двух условных
граничных слоев соответствующей толщины.
Общее термическое сопротивление теплопередачи через такую стенку:
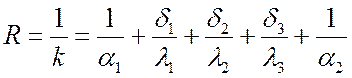 .
.
Отложим на горизонтали отрезки O1A1, A1A2, A2A3, A3A4, A4O2, равным термическим сопротивлениям ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В точках O1,
A1, A2, A3, O2 восстановлен
перпендикуляр. На O1K1
и O2K2 отложим
в масштабе температуры tж1
и tж2. Соединим прямой
точки C1 и B2.
. В точках O1,
A1, A2, A3, O2 восстановлен
перпендикуляр. На O1K1
и O2K2 отложим
в масштабе температуры tж1
и tж2. Соединим прямой
точки C1 и B2.
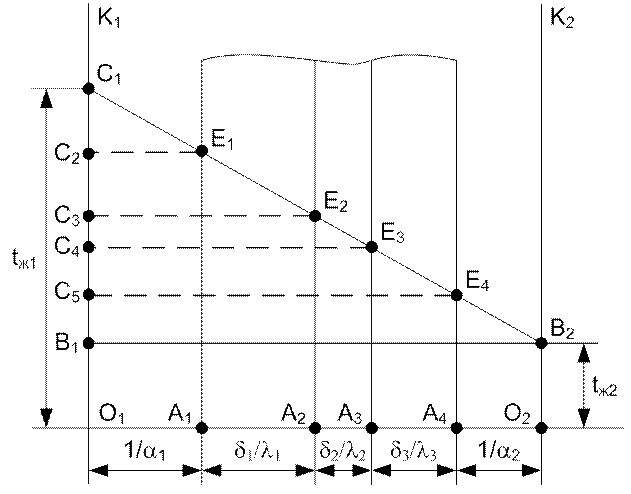
Рис. 11. Графический метод расчета температур
Отрезки A1E1, A2E2, A3E3 и A4E4 будут равны искомым температурам tc1, tc2, tc3, tc4.
Из подобия треугольников C1B1B2 и C1C2E1 следует, что:
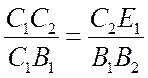 , или
, или 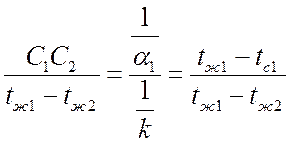 .
.
Причем:
![]() ,
, 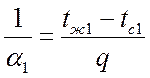 ,
,
![]() ,
, 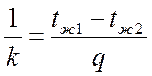 ,
,
Тогда:
![]() ,
, ![]() .
.
Аналогично можно доказать, что и отрезки A2E2, A3E3 и A4E4 будут соответственно равны tc2, tc3 и tc4.
Рассмотрим случай, когда при передаче тепла через
однородную изотропную стенку на одной поверхности заданы граничные условия
второго рода в виде ![]() при x
= 0, а на другой поверхности заданы коэффициент теплоотдачи a2 и температура окружающей
среды tж2 – граничные
условия третьего рода. Внутренние источники в стенке отсутствуют (qv = 0).
при x
= 0, а на другой поверхности заданы коэффициент теплоотдачи a2 и температура окружающей
среды tж2 – граничные
условия третьего рода. Внутренние источники в стенке отсутствуют (qv = 0).
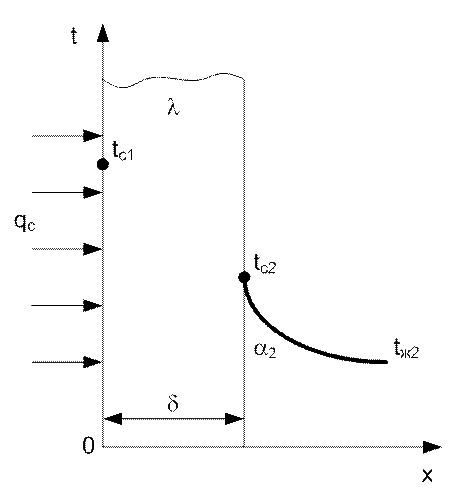
Рис. 12. Теплопроводность с граничными условиями второго и третьего рода
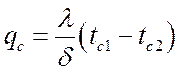 ,
,
![]() .
.
При заданном значении qc:
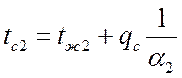 ,
,
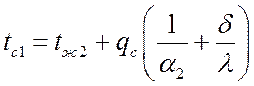 .
.
При многослойной стенке из n слоев для правой внешней поверхности:
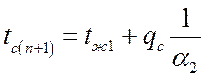 ,
,
для внешней левой поверхности:
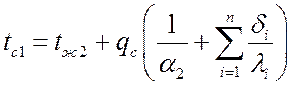 .
.
Рассмотрим теплопроводность однослойной цилиндрической стенки в условиях стационарного температурного поля: qv = 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.