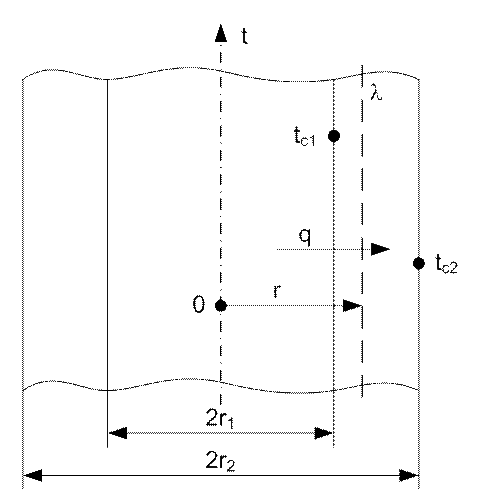
Рис. 13. Теплопроводность цилиндрической стенки
В цилиндрических координатах уравнение теплопроводности имеет вид:
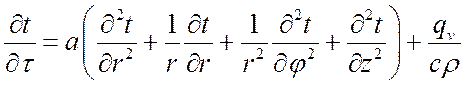 ,
,
где r – радиус-вектор в цилиндрической системе координат;
j – угол радиус-вектора.
Заданы: tc1 и tc2, l = const.
Определить распределение температур в стенке при одномерном температурном поле.
Для одномерного поля:
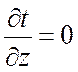 ,
, 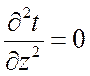 .
.
Поскольку изотермические поверхности имеют общую с трубой ось и являются цилиндрами, то температура вдоль j не должна изменяться, т. е.
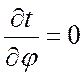 ,
, 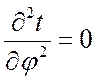 .
.
С учетом этого уравнение теплопроводности примет вид:
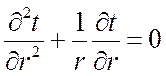 . (*)
. (*)
Граничные условия:
при
![]()
![]() ,
,
при ![]()
![]() .
.
Введем новую переменную 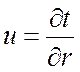 .
Тогда:
.
Тогда:
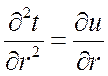 ,
, 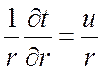 .
.
Подставим эти выражения в уравнение (*). Получим:
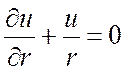 ,
,
или
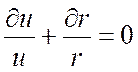 .
.
Интегрируем:
![]() .
.
Потенцируем:
![]() ,
,
или
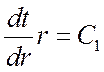 ,
, 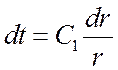 .
.
Интегрируем:
![]() . (**)
. (**)
При ![]()
![]() ,
,
![]() .
.
При ![]()
![]() ,
,
![]() .
.
Решение этих уравнений дает:
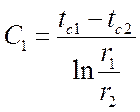 ,
, 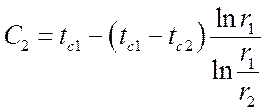 .
.
Подставляя C1 и C2 в уравнение (**), получим:
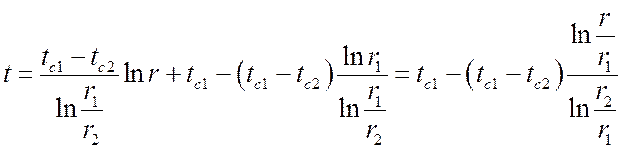 , °C,
, °C,
или
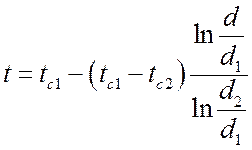 , °C.
, °C.
Это уравнение есть уравнение логарифмической кривой.
Для определения теплового потока запишем закон Фурье:
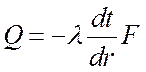 ,
, ![]() .
.
Градиент температуры:
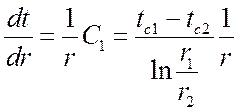 .
.
Тогда:
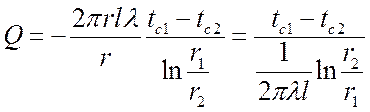 , Вт.
, Вт.
Тепловой поток на единицу длины трубы (на 1 м):
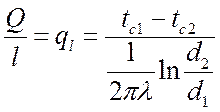 , Вт/м,
, Вт/м,
где ql – линейная плотность теплового потока.
Тепловой поток на единицу внутренней поверхности:
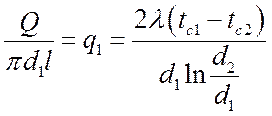 ,
Вт/м2.
,
Вт/м2.
Тепловой поток на единицу внешней поверхности:
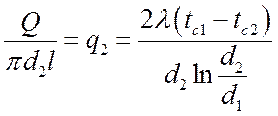 ,
Вт/м2.
,
Вт/м2.
Связь между ними:
![]() , Вт/м.
, Вт/м.
В том случае, когда коэффициент теплопроводности материала
стенки является функцией температуры ![]() , то линейная плотность
теплового потока может быть определена по формуле, что и для l = const:
, то линейная плотность
теплового потока может быть определена по формуле, что и для l = const:
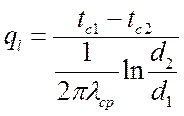 ,
,
где lср – среднеинтегральное значение коэффициента теплопроводности:
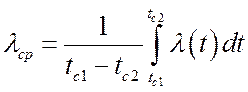 .
.
Для цилиндрической стенки при ![]() :
:
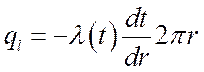 .
.
Разделив переменные и проинтегрировав в пределах от ![]() до r и от
до r и от ![]() до t,
получим выражение температурного поля цилиндрической стенки при
до t,
получим выражение температурного поля цилиндрической стенки при ![]() :
:
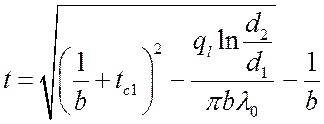 .
.
При стационарном температурном поле линейная плотность теплового потока ql не зависит от толщины стенки, т. е.
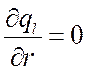 .
.
Тогда для многослойной стенки, состоящей из n слоев:
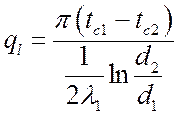 ,
, 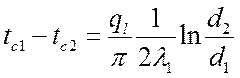 ,
,
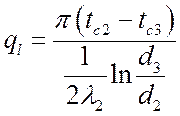 ,
, 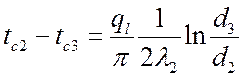 ,
,
…
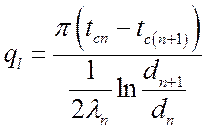 ,
,
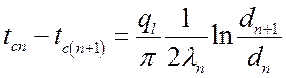 ,
,
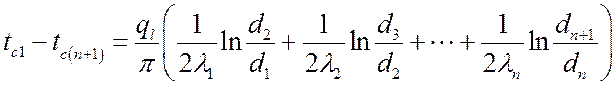 .
.
Тогда:
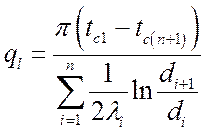 .
.
Величина 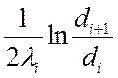 , (м·K)/Вт,
называется линейным термическим сопротивлением отдельного слоя, а величина
, (м·K)/Вт,
называется линейным термическим сопротивлением отдельного слоя, а величина 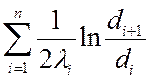 – полным линейным термическим
сопротивлением.
– полным линейным термическим
сопротивлением.
Формулы нахождения температур на границах слоев:
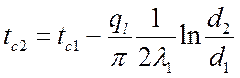 ,
,
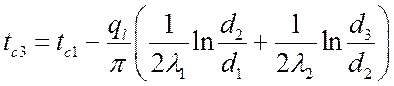 ,
,
…
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.