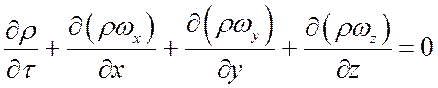Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 29

                                     .                                                                  (15)

Для несжимаемых жидкостей ():

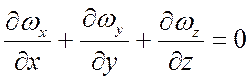                                      , или . (16)

5.2.4. Уравнения конвективного теплообмена

Таким образом, имеем следующие дифференциальные уравнения при конвективном теплообмене:

1. Уравнение энергии

1.1. Для несжимаемых жидкостей ( ()

           ,

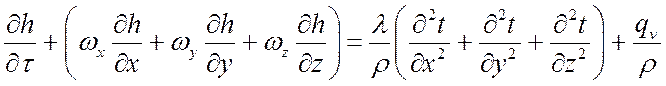или

                                 .

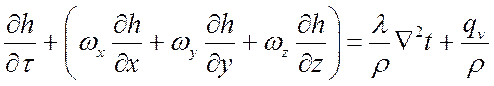1.2. Для идеальных газов ():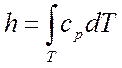

          ,

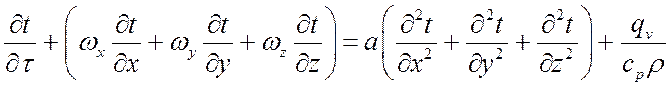или при :

                                                      .

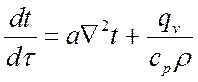2. Уравнение движения:

                                              .

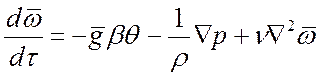3. Уравнение сплошности:

3.1. Для несжимаемых жидкостей (:

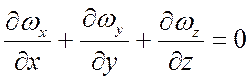                                      , или .

3.2. Для газов и паров:

                                     .

6. Основы теории подобия

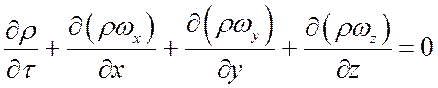При изучении явления теплообмена при конвективной теплоотдаче сталкиваемся как с самим явлением теплообмена, так и с сопутствующими гидродинамическими явлениями. Вся совокупность явлений описывается системой дифференциальных уравнений, в которую входят: уравнение теплопроводности (теплообмена), уравнение энергии (движения), уравнение сплошности (неразрывности). Кроме того, задаются краевые условия или условия однозначности, определяющие частные условия теплообмена. К ним относятся: геометрические условия, физические условия, граничные условия, временные условия. Система дифференциальных уравнений и условия однозначности создают математическое описание теплообмена при конвективной теплоотдаче.

Вследствие ограниченности аналитического решения дифференциальных уравнений большое значение приобретает эксперимент в изучении сложного процесса. При постановке эксперимента ставится другая задача: получить данные для расчета других процессов, родственных изучаемому. Средством решения такой задачи является теория подобия, являющейся теорией эксперимента.

Теория подобия – это учение о подобии явлений. Впервые с подобием треугольников мы встречаемся в геометрии:

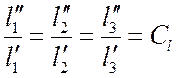                                                        .                    (1)

где   , ,  – линейные размеры одной фигуры;

        , ,  – линейные размеры другой фигуры;

        C_l – коэффициент пропорциональности, или постоянная геометрического подобия.

Таким образом, условие (1) является условием геометрического подобия.

Можно говорить и о подобии движения двух потоков жидкости – кинематическом подобии, о подобии сил, вызывающих подобные между собой движения – динамическом подобии, о подобии распределения температур и тепловых потоков – тепловом подобии и т. д.

Понятие подобия физических явлений сводится к следующим положениям:

а) физические явления подобны, если они одного и того же рода, качественно одинаковы и описываются одними и теми же дифференциальными уравнениями как по форме, так и по содержанию. Если математическое описание явлений одинаково по форме, но различно по содержанию, то такие явления будут называться аналогичными, но не подобными. Например: процессы теплопроводности, электропроводности и диффузии аналогичны;

б) обязательной предпосылкой подобия физических явлений должно быть геометрическое подобие, т. е. подобные явления протекают в геометрически подобных системах;

в) при анализе подобных явлений сопоставлять между собой можно только однородные величины и лишь в сходственных точках пространства и в сходственные моменты времени.

Однородными величинами называются такие величины, которые имеют один и тот же физический смысл и одинаковую размерность. Сходственными точками пространства геометрически подобных систем называются такие координаты, которые удовлетворяют условию (1):

                                            ; ; .

Сходственными моментами времени называются такие, которые имеют общее начало отсчета и связаны преобразованием подобия:

                                                             .