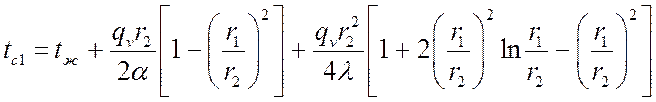Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 21

            .

Если заданы граничные условия первого рода, т. е. температура поверхности t_c2, то задачу можно рассматривать при , т. е. когда . Тогда можно записать:

                                     .

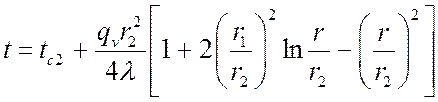Полагая в уравнении  и , можно найти перепад температур в стенке:

                                         .

3.9.3.2. Тепло отводится только через внутреннюю поверхность трубы

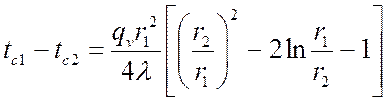Заданы: коэффициент теплоотдачи a на внутренней поверхности и температура среды внутри трубы t_ж. Граничные условия:

                                          при  ;

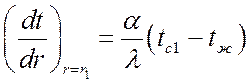                                                  при  .

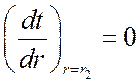Аналогично предыдущему пункту 3.8.3.1 определяются постоянные C₁ и C₂ в уравнении:

                                                  .

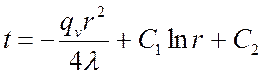После определения постоянных и подстановки получим:

                 .

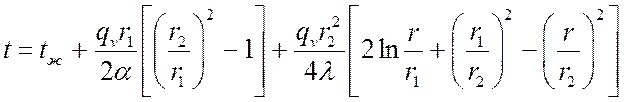Перепад температур между стенкой и жидкостью:

                                               .

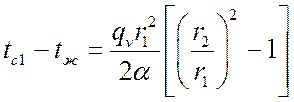Если задана температура на теплоотдающей поверхности t_c1, что соответствует случаю , уравнение примет вид:

                                      .

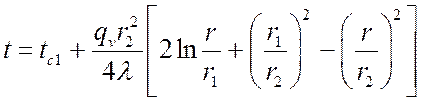Если , что соответствует , получим полный температурный напор в стенке:

                                         .

3.9.3.3. Тепло отводится через внутреннюю и наружную поверхности

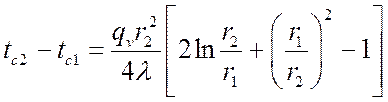В этом случае в стенке должен существовать максимум температур. Изотермическая поверхность, соответствующая максимальной температуре t₀, разделяет цилиндрическую поверхность на два слоя. Во внутреннем слое тепло передается внутрь трубы, во внешнем слое – наружу. Максимальное значение температуры соответствует условию 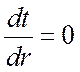, т. е. .

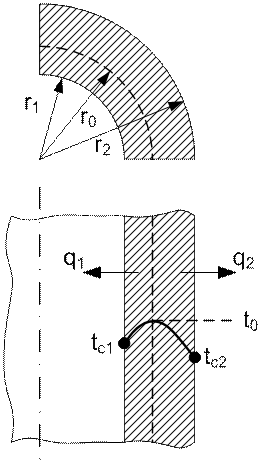
Рис. 29. Теплоотвод через обе поверхности трубы

Из п. 3.9.3.2 падение температуры в стенке:

                                         .

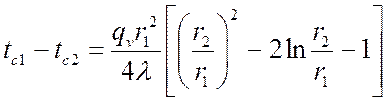Для нашего случая:

                                         ;     (*)

                                         .    (**)

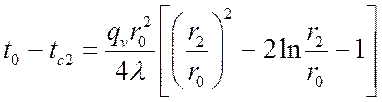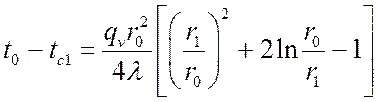Вычитая правые и левые части уравнений, получим:

                             .

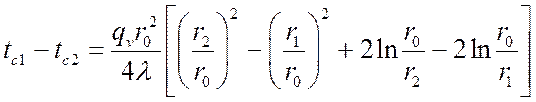Решив уравнение относительно r₀, получим:

                                              ,       (***)

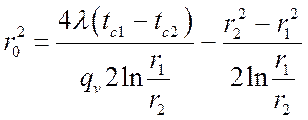или

                                           .    (***)

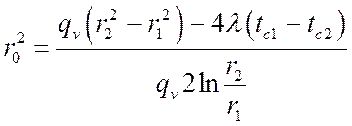Подставив это выражение в (*) или (**), получим максимальную температуру.

Распределение температуры во внутреннем слое определится, если в уравнение п. 3.9.3.2 подставить текущую координату :

                                      .

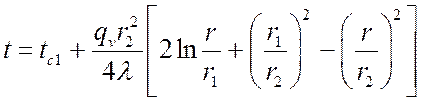Подставив значение радиуса r в интервале  в выражение температуры п. 3.8.3.1, получим распределение температуры для наружного слоя:

                                     .

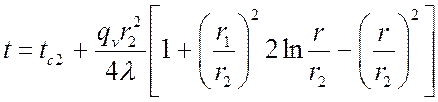Если температуры внутренней и внешней поверхностей одинаковы, то выражение для r₀ упрощается:

                                                          ,

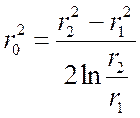т. е. r₀ зависит только от размеров стенки, и не зависит от тепловых условий. Например, при r₂ = 2 и r₁ =1 r₀ = 1,46.

Если известны граничные условия третьего рода: t_ж1и t_ж2, a₁ и a₂, а неизвестны t_c1 и t_c2, то для определения r₀ добавляются уравнения:

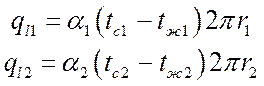                              , где .                                                                (****)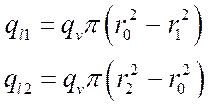

Для определения r₀ нужно совместно решить уравнения (****) и (***) относительно r₀.

4. Теплопроводность при нестационарном режиме

4.1. Общие представления

Процессы теплопроводности, когда температурное поле изменяется не только в пространстве, но и во времени, называются нестационарными. Они существуют в технике, быту. Например, нагрев или охлаждение заготовок и изделий, в производстве стекла, обжиге кирпича, вулканизации резины, пуске или останове теплосилового оборудования и т. д.

Все процессы нестационарной теплопроводности можно сосредоточить в две группы: 1) процессы, в которых тело стремится к тепловому равновесию; 2) процессы, в которых температурное поле тела претерпевает периодические изменения. К первой группе относятся такие процессы, как нагрев или охлаждение болванки до состояния равновесия, ко второй – периодический нагрев и охлаждение стенки теплового регенератора, применяемого для нагрева воздуха в МГД-установках.