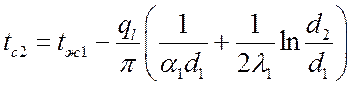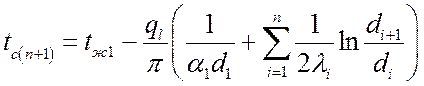Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 14

                                           ,

                                                                   …

                                      .

При задании граничных условий первого рода положим, что  и , а t_ж1 и t_ж2 соответственно равны t_c1 и t_c2, тогда:

                                                      .

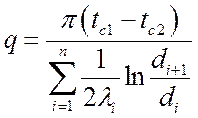Температуры на границах между слоями:

                                               .

3.3. Критический диаметр изоляции

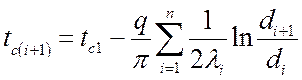При постоянных значениях a₁, d₁, l и a₂ термическое сопротивление цилиндрической стенки зависит от внешнего диаметра d₂:

                                 .

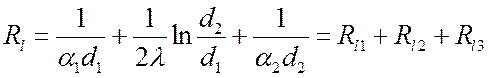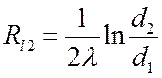При a₁, d₁, l, a₂ = const термическое сопротивление . Термическое сопротивление  с увеличением d₂ будет увеличиваться, а термическое сопротивление 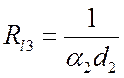 – уменьшаться. Полное же сопротивление R_l будет определяться степенью влияния R_l2 и R_l3. Изменение R_l1, R_l2, R_l3 и R_l показано на рис. 15.

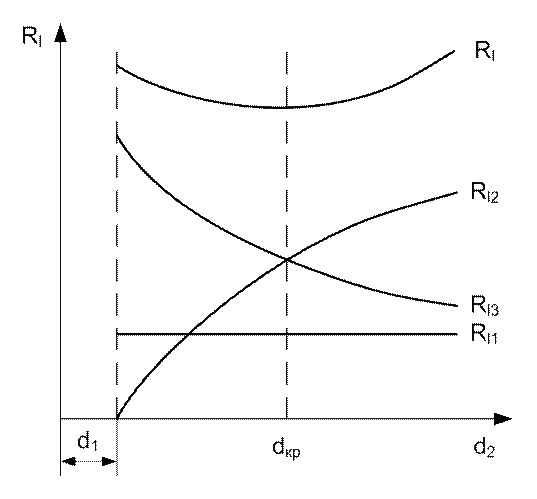
Рис. 15. Изменение составляющих термического сопротивления

Чтобы исследовать влияние d₂ на R_l, возьмем первую производную:

                                               .

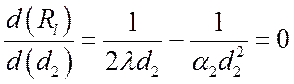Это соответствует точке перегиба кривой R_l, значение диаметра d₂ в которой называется критическим:

                                                              ,

                                                      .

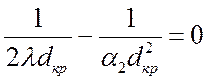Отсюда

                                                             .

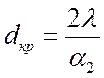При  с увеличением d₂ R_l падает, т. к. R_l3 падает интенсивнее, чем увеличивается R_l2. Но при  падение R_l3 становится менее интенсивно, чем увеличение R_l2, и поэтому R_l увеличивается.

Это обстоятельство можно распространить и на случай, когда труба покрыта слоем изоляции.

Рис. 16. Труба с изоляцией

                                    ,

                                                      .

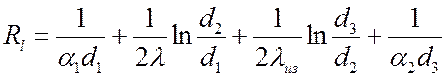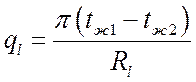При увеличении d₃ при  q_l будет сначала возрастать, т. к. R_l падает, при  q_l будет иметь максимум, а при  q_l будет падать.

                                                            .

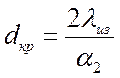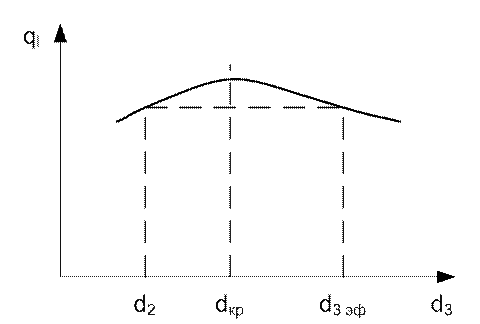
Рис. 17. Зависимость теплового потока от толщины изоляции

Таким образом, наложение слоя тепловой изоляции толщиной в области  приводит к увеличению тепловых потерь, превышающих тепловые потери с оголенного трубопровода. При  тепловые потери достигнут максимума. Только лишь при  тепловые потери сравняются с тепловыми потерями оголенного трубопровода. Для эффективной тепловой защиты необходимо, чтобы . Но это сопряжено с увеличением расхода изоляционного материала. Окончательное решение о величине d₃ следует принимать, исходя из экономических соображений.

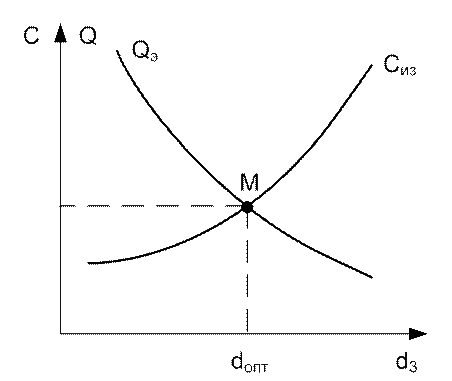
Рис. 18. Экономическая эффективность изоляции

C_из – стоимость изоляции; Q_э – стоимость сэкономленного тепла

При увеличении d₃ C_из возрастает, Q_э уменьшается, точка пересечения определит значение оптимального диаметра изоляции d_опт и нормативные тепловые потери Q_норм.

Задача оптимизации выбора конструкции изоляции может быть решена и с учетом теплофизических свойств изоляционного материала. С целью ее решения при проектировании проводят расчеты при различных материалах изоляции, т. е. с различными l_из. Тогда будут варьироваться d_кр. Рекомендация: для эффективной работы изоляции необходимо стремиться, чтобы , т. е. .

Пример: труба d₂ = 20 мм покрывается изоляцией, в качестве которой используют асбест с l = 0,1 Вт/(м·K) при коэффициенте теплоотдачи a₂ = 5 Вт/(м²·K). Целесообразно ли использовать этот материал?

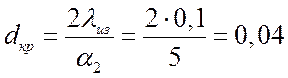                                               м.

Т. к. , то асбест использовать нецелесообразно.

3.4. Передача тепла через шаровую стенку

Определим тепловой поток теплопроводностью через стенку полого шара с радиусами r₁ и r₂, имеющей коэффициент теплопроводности l. Стенка однородна и изотропна.

3.4.1. Граничные условия первого рода

Рис. 19. Теплопроводность шаровой стенки

Запишем закон Фурье:

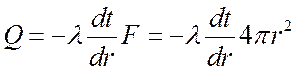                                            , Вт.

Запишем граничные условия:

                                                       при  ,

                                                       при  .

Разделим переменные: