Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 46

Выпадение дождя – тоже есть процесс конденсации. Для этого пар должен быть пересыщен (его плотность должна превышать плотность насыщенного пара). Мерой пересыщения служит отношение . Если 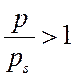 – пар пересыщен, при  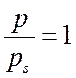– насыщен. Степень пересыщения зависит от наличия в паре зародышей конденсации: пылинок-аэрозолей, электрически заряженных частиц (ионизированные атомы).

8.2. Теплоотдача при пленочной конденсации

Тепло, выделяющееся на внешней границе пленки конденсата, отводится к поверхности охлаждения. При ламинарном движении пленки конденсата перенос тепла через нее затруднен и будет осуществляться лишь теплопроводностью. Сравните:  Вт/(м·K) при  бар,  °C;  Вт/(м·K).

Если принять, что температура частиц конденсата, соприкасающихся с паром, равна температуре насыщения, то поток тепла по закону Фурье:

                                                         ,

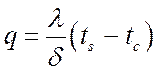где   d – толщина конденсатной пленки;

        l – коэффициент теплопроводности конденсата;

        t_c – температура стенки.

С другой стороны, тепловой поток от пара к пленке:

                                                         .

Отсюда имеем:

                                                               .

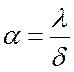Следовательно, задача сводится к отысканию величин d при различных условиях движения пленки конденсата, а l – теплофизическая величина, которая может быть просто определена из таблиц.

Впервые Нуссельт провел анализ процесса конденсации пара на вертикальной стенке и горизонтальной трубе.

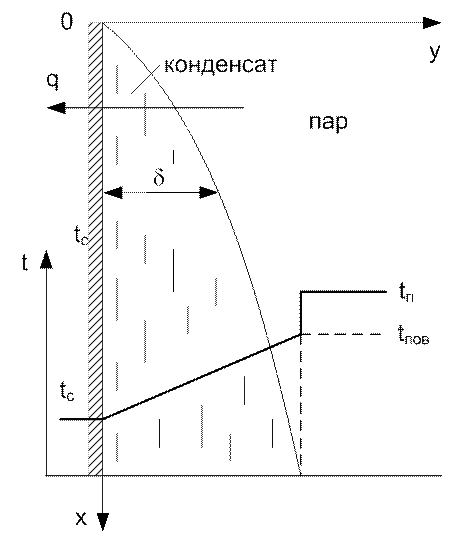
Рис. 86. Конденсация на вертикальной стенке

Дифференциальное уравнение движения для единицы объема конденсата в пленке имеет вид:

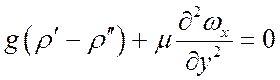                                                ,           (18)

т. е. сила тяжести уравновешивается силой вязкости, действующей со стороны соседних слоев жидкости. Силы инерции из-за их малости в решении Нуссельта не учитываются.

Интегрирование (18) приводит к соотношению:

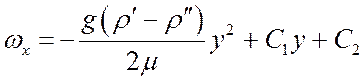                                          .     (19)

При  , при  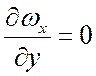, отсюда: , 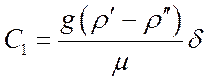. Подставим C₁ и C₂ в уравнение (19), получим закон распределения скоростей в слое конденсата:

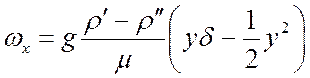                                              .         (20)

Количество жидкости, протекающей в единицу времени через сечение x при ширине плиты, равной единице, определится формулой:

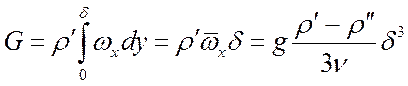                                       ,  (21)

где   .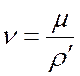

Отсюда:

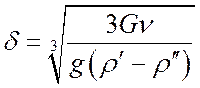                                                      ,                (22)

т. е. d увеличивается с ростом расхода жидкости в пленке в кубической степени.

Расход конденсата может быть определен и из уравнения теплового баланса:

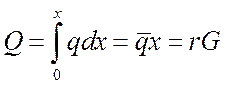                                                    ,               (23)

где   Q – поток тепла, передаваемый стенке на участке 0 – x при ширине плиты, равной единице.

Используя величины q и G, получим:

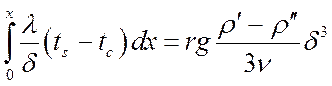                                             .       (24)

Здесь одна неизвестная величина d – толщина пленки. Поскольку при  d должна быть тоже равна нулю, то решение уравнения (24) ищем в виде:

                                                              .

Подставив это выражение в (24), имеем:

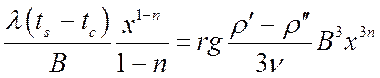                                         .    (25)

Соотношение (25) должно выполняться при любом x, следовательно, показатели степени x слева и справа должны быть одинаковы. Отсюда:

                                                      ; .

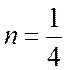Тогда из (25):

                                                    .

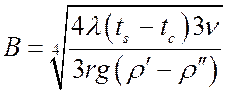Окончательно:

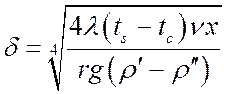                                                    .              (26)

Учитывая, что 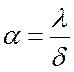, получаем локальный коэффициент теплоотдачи:

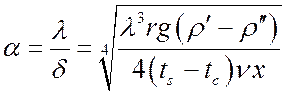                                                .          (27)

Осреднение для случая вертикальной стенки или вертикальной трубы высотой h:

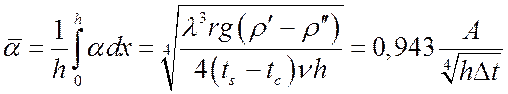                                ,                                                                  (28)

где   ; .

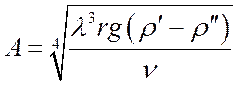Из (28) следует, что величина  уменьшается с ростом h и температурного напора Dt.

Полученные формулы применимы и для наклонной стенки: изменение учитывается величиной , где y – угол наклона стенки: