Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 51

или

                                                   ,

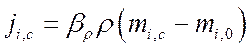где   j_i,c – плотность потока массы, кг/(м²·K);

        b – коэффициент массоотдачи, отнесенной к разности концентраций диффундирующего вещества, м/с.

        индексы «c» и «0» указывают, что концентрация диффузионного вещества берется соответственно на поверхности раздела фаз и вдали от нее.

Используя уравнение идеальных газов , уравнение массоотдачи можно записать в виде:

                                       ,

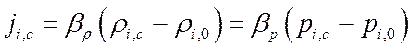или

                                                    ,

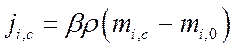где   b_p – коэффициент массоотдачи, отнесенный к разности парциальных давлений , т. е.:

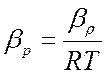                                              ; , с/м.

Рассмотрим испарение жидкости в парогазовую среду. Не учитываем термо- и бародиффузию, т. к. полагаем, что температурная разность компонентов парогазовой смеси ничтожна, и давление по всему объему неизменно.

Концентрация пара m_п.с на поверхности жидкости изменяется до значения m_п.0 вдали от поверхности. Но сумма концентраций , поэтому:

                                                          .

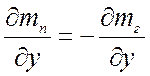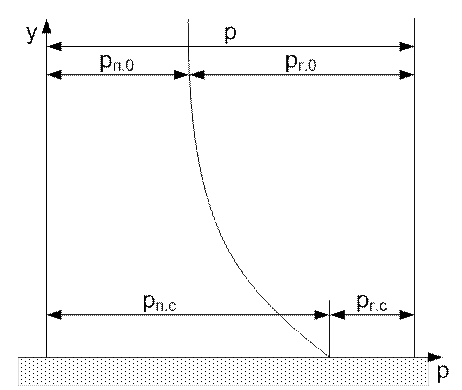
Рис. 89. Распределение давлений в парогазовой смеси

Диффузионный поток массы пара направлен в сторону убыли концентрации, т. е. от поверхности. Пар диффундирует в парогазовую среду свободно. Газ же должен диффундировать в обратном направлении (к поверхности). Но поверхность является непроницаемой для газа преградой, и поэтому концентрация газа у поверхности должна возрастать непрерывно, чего нет на самом деле. Это несоответствие компенсируется конвективным компенсирующим потоком парогазовой смеси около поверхности, который называют стефановым потоком. Его скорость w_с.п. Следовательно, суммарный поток пара равен сумме молекулярного и конвективного стефановского потоков пара:

                                           .

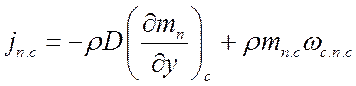Запишем по аналогии для газа:

                                           ,

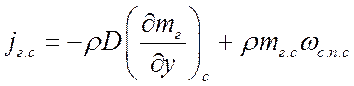но для газа жидкость является преградой, и поэтому суммарный поток газа равен нулю, т. е.:

                                                 ,

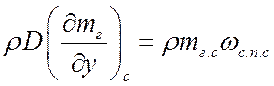или с учетом того, что :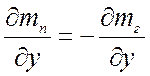

                                                .

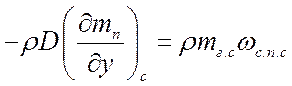Тогда:

                                                   .

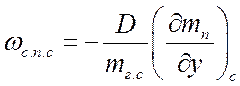Подставим в формулу j_п.с, получим:

                              ,

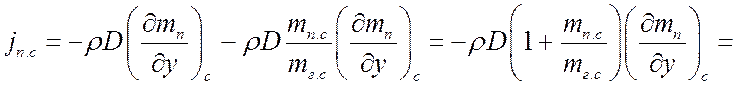
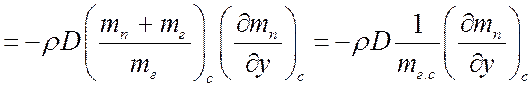т. к. для бинарной смеси .

Выражение j_п.с отличается от обычного выражения закона Фика 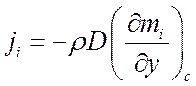 сомножителем 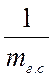, учитывающим конвективный стефанов поток, вызванный непроницаемостью поверхности испарения для газа. Стефанов поток появляется и при отсутствии свободной и вынужденной конвекции.

Поток массы пара от поверхности испарения:

                                                   ;

                                                  .

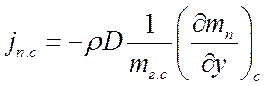Отсюда коэффициент массоотдачи:

                                               .

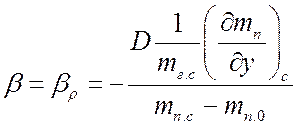Рассмотренный пример соответствует условиям полупроницаемой поверхности, т. е. такой, которая пропускает один (активный) компонент смеси (пар), но не пропускает инертный компонент (газ). Этот же вид поверхности наблюдается и для конденсации пара.

Полностью проницаемая поверхность, когда она проницаема для обоих компонентов бинарной смеси (например, конденсация обоих компонентов смеси).

Принимая аналог с теплообменом:

                                       и ,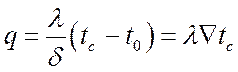

для массообмена имеем:

                                                       .

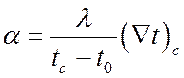При полупроницаемой поверхности в условиях стационарного процесса стефанов поток компенсирует встречный молекулярный поток газа, и реально возникает лишь поперечный поток пара. В этом случае на границе раздела фаз имеем при испарении:

                                                  .

Общее количество тепла q_c, отдаваемое или воспринимаемое жидкостью и парогазовой смесью, равно сумме теплоты, переданной конвективным теплообменом, и теплоты, переданной диффундирующей массой в виде энтальпии.

9.4. Диффузионный пограничный слой