2) Равнодействующая сил давления df2:
если на верхней грани элемента действует давление p,
то на площадку ![]() действует сила
действует сила ![]() . На нижнюю грань действует давление с
точностью до второго члена разложения в ряд Тейлора:
. На нижнюю грань действует давление с
точностью до второго члена разложения в ряд Тейлора: 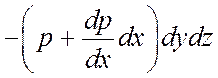 .
Знак «–» указывает на то, что сила направлена против движения.
.
Знак «–» указывает на то, что сила направлена против движения.
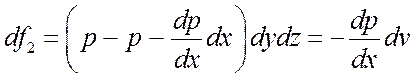 .
.
3) Сила трения возникает на боковых поверхностях элемента. Т. к. скорость wx изменяется только в направлении оси Oy, то сила трения, направленная против течения, будет равна алгебраической сумме:
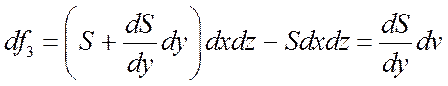 .
.
Сумма этих сил есть равнодействующая всех сил, приложенных
к элементу (с учетом того, что  и касательная сила
и касательная сила 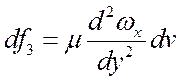 ):
):
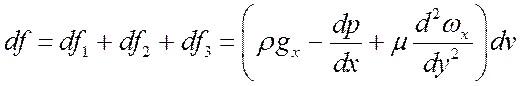 . (4)
. (4)
С учетом сил инерции на основании второго закона механики равнодействующая df
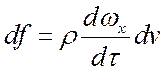 (5)
(5)
равна произведению массы элемента ![]() на его
ускорение
на его
ускорение 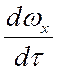 .
.
Приравнивая (4) и (5), получаем уравнение движения вдоль оси Ox:
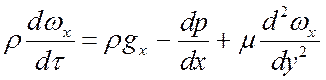 . (6)
. (6)
По аналогии, для трехмерного течения несжимаемой жидкости с постоянными физическими параметрами:
ось Ox:
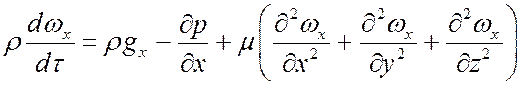 ; (7)
; (7)
ось Oy:
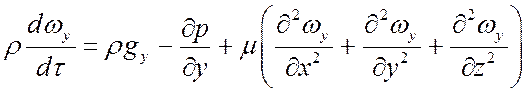 ; (8)
; (8)
ось Oz:
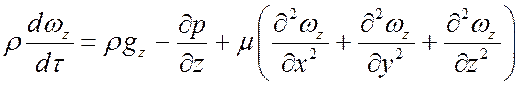 ; (9)
; (9)
Уравнения (7) – (9) называются уравнениями Навье-Стокса. Все слагаемые имеют размерность силы, отнесенной к единице объема: Н/м3.
Представим левые части уравнений (7) – (9) как полные производные:
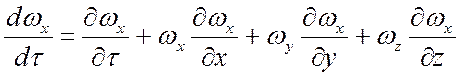 ; (10)
; (10)
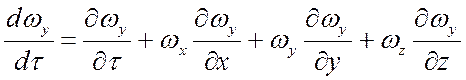 ; (11)
; (11)
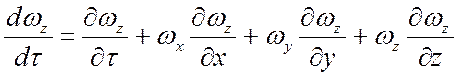 . (12)
. (12)
В уравнениях (10) – (12) производные 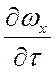 ,
, 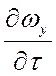 ,
,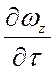 характеризуют изменение скорости во
времени в какой-либо точке (локальное изменение), а остальные слагаемые –
изменение скорости при переходе из одной точки в какую-либо другую
(конвективное изменение скорости). Используя векторную форму записи, получим:
характеризуют изменение скорости во
времени в какой-либо точке (локальное изменение), а остальные слагаемые –
изменение скорости при переходе из одной точки в какую-либо другую
(конвективное изменение скорости). Используя векторную форму записи, получим:
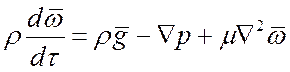 . (13)
. (13)
Это уравнение движения.
Если в этом уравнении учесть изменение плотности среды во времени от воздействия температуры среды через коэффициент объемного расширения:
![]() ,
,
где ![]() , то уравнение движения примет
вид:
, то уравнение движения примет
вид:
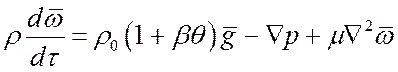 ,
,
или в конечном итоге:
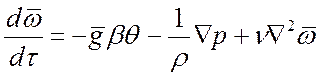 . (14)
. (14)
Т. к. в уравнение (14) входит неизвестная величина давления p, то система не замкнутая. Необходимо еще одно уравнение – уравнение сплошности.
Выделим в потоке жидкости неподвижный параллелепипед со сторонами dx, dy, dz и подсчитаем массу жидкости, проходящей через него за время dt.
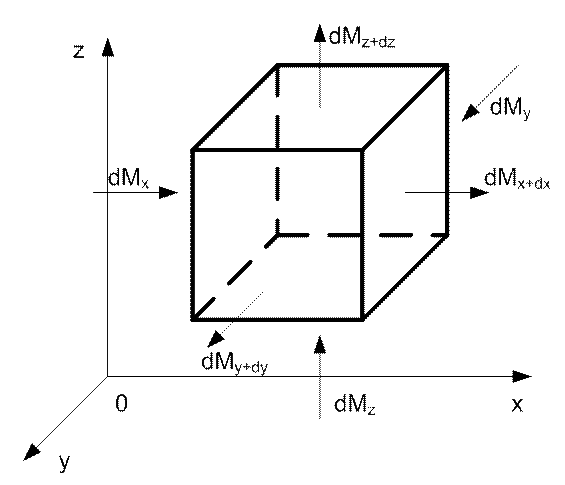
Рис. 41. К выводу уравнения сплошности
В направлении оси Ox втекает масса:
![]() , (*)
, (*)
а вытекает:
![]() .
.
Ограничиваясь разложением в виде двух первых членов ряда,
получим массу ![]() по оси Ox
в виде:
по оси Ox
в виде:
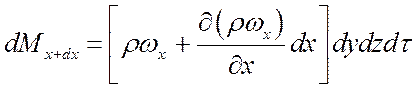 . (**)
. (**)
Вычитая из (**) выражение (*), получим излишек вытекающей из элементарного объема массы:
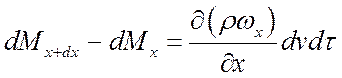 . (а)
. (а)
Аналогично в направлении других осей:
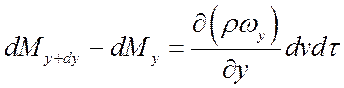 . (б)
. (б)
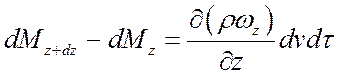 . (в)
. (в)
Суммируя по трем осям, получаем избыток массы,
обусловленный изменением плотности жидкости в объеме dv,
который равен изменению массы данного объема во времени 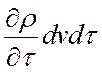 .
Тогда окончательный вид уравнения сплошности жидкостей:
.
Тогда окончательный вид уравнения сплошности жидкостей:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.