Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 19

В ряде случаев внутри расчетных объектов могут протекать процессы, в результате которых будет выделяться или поглощаться тепло. Например, выделение джоулева тепла при прохождении электрического тока по проводникам, объемное выделение тепла в тепловыделяющих элементах атомных реакторов, выделение тепла при протекании химических реакций и т. д.

Интенсивность выделения (поглощения) тепла характеризуется плотностью объемного тепловыделения q_v, Вт/м³. Если q_v положительна, то в теле имеются положительные источники тепла. В стоках тепла q_v отрицательна.

Источники внутреннего тепловыделения подразделяются на точечные, линейные, поверхностные, объемные.

Дифференциальное уравнение для стационарного режима 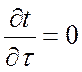 при наличии внутренних источников тепла имеет вид:

                                                          .

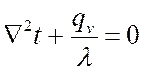Рассмотрим несколько случаев теплообмена.

3.9.1. Теплопроводность однородной пластины

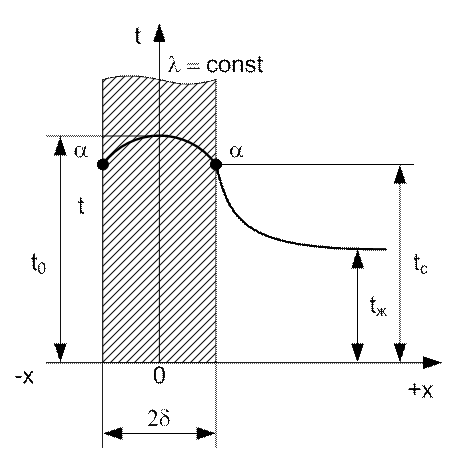
Рис. 26. Теплопроводность однородной пластины

Толщина пластины 2d – величина малая по сравнению с другими размерами. Источники тепла распределены равномерно по всему объему и равны . Заданы:  – коэффициент теплоотдачи,  – температура вдали от пластины. Вследствие равномерного охлаждения температуры обоих поверхностей одинаковы. При этих условиях температура вдоль оси x будет изменяться. Неизвестны температуры t₀ на оси пластины и t_c на поверхности. Необходимо найти распределение температур по оси x и найти количество отданного тепла.

Принимая решение задачи одномерного поля, дифференциальное уравнение примет вид:

                                                          .

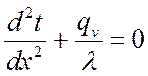Граничные условия:

                                      при  .

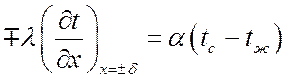Поскольку граничные условия для обеих сторон пластины одинаковы, температурное поле будет симметричным относительно плоскости . Можно рассмотреть одну половину, например, правую.

Тогда граничные условия можно записать:

                                                       ;

                                            .

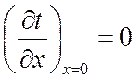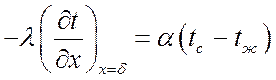После интегрирования получим:

                                                       ,

                                                   .               (*)

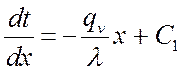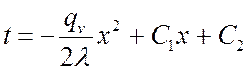Из граничных условий:

                                      при  , ;

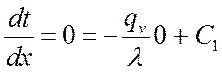                    при  , .

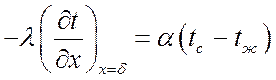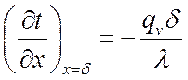Тогда:

                                                          .

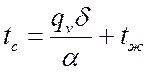Подставив это выражение в уравнение (*) при , получим:

                                            ,

                                                   .

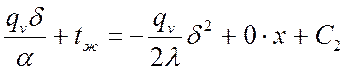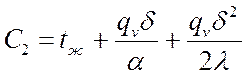Используя C₁ и C₂, получим:

                                     ,

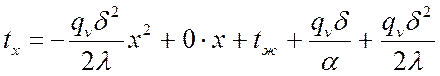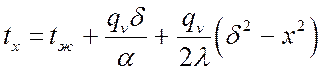                                          , °C.

Тепловой поток изменяется вдоль оси x:

                                                              ,

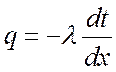                                                 – закон Фурье.

При  , т. к. при  .

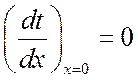Тепловой поток с единицы поверхности пластины при :

                                              , Вт/м²,

а общее количество тепла, отдаваемое всей поверхностью в единицу времени:

                                                   , Вт,

т. к. вся поверхность F равна двум боковым F₁.

Если предположить симметричное распределение температуры в пластине по параболическому закону и положить , то температурное поле будет такое же, как и для граничных условий первого рода, поскольку при  , тогда:

                             .

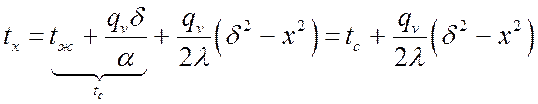При этом температура на оси симметрии ():

                                                         ,

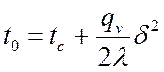а перепад температур между осью симметрии и ее поверхностью:

                                                         .

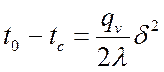В случае учета зависимости  уравнение температурной кривой имеет вид:

                                              .

3.9.2. Теплопроводность однородного цилиндрического стержня

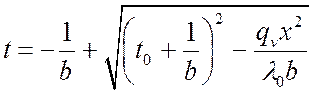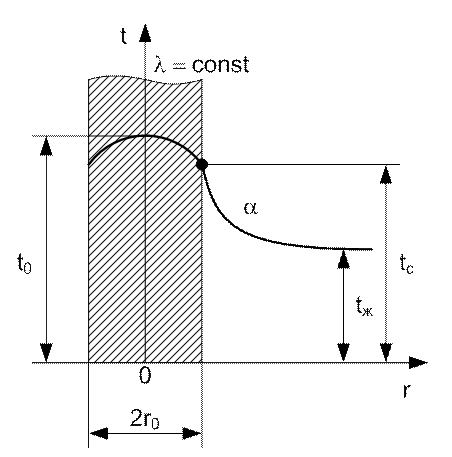
Рис. 27. Теплопроводность однородного цилиндрического стержня

Имеем цилиндр, радиус которого мал по сравнению с длиной цилиндра. Поэтому температура будет изменяться только вдоль радиуса. Внутренние источники распределены равномерно. Заданы:  – температура окружающей среды,  – постоянный по всей поверхности коэффициент теплоотдачи. Температура во всех точках поверхности будет одинакова.