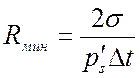 ,
,
где 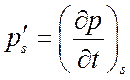 – производная давления по
температуре на линии насыщения – физическая характеристика вещества.
– производная давления по
температуре на линии насыщения – физическая характеристика вещества.
Согласно закону Клапейрона-Клаузиуса:
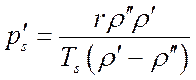 , Н/(м2·K),
, Н/(м2·K),
где r¢ и r² – плотность жидкости и пара соответственно;
Ts – абсолютная температура насыщения, K;
r – теплота парообразования.
Отсюда с учетом зависимости давления от кривизны поверхности раздела фаз:
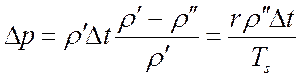 .
.
Тогда:
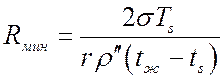 .
.
Если положить, что слои жидкости, прилегающие к стенке, имеют температуру tc, то:
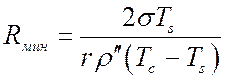 .
.
Анализ формулы показывает, что с увеличением давления (растет r²) и перегрева Dt при заданном давлении Rмин уменьшается, а следовательно, растет общее число действующих центров парообразования, интенсифицируется перемешивание жидкости в пограничном слое и увеличивается теплоотдача.
К наиболее благоприятным условиям образования парового пузырька относятся условия, при которых работа образования пузырьков критического размера будет минимальной. Работа образования пузырька в объеме жидкости выражается:
![]() ,
,
где V и F – объем и поверхность пузырька;
sF – работа образования межфазной поверхности.
Чем меньше работа, тем больше вероятность вскипания, т. к.
последняя пропорциональна 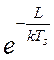 , где k = 1,38044·10–23
Дж/K – постоянная Больцмана.
, где k = 1,38044·10–23
Дж/K – постоянная Больцмана.
Объем пузырька 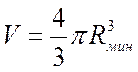 , поверхность
, поверхность ![]() . Таким образом:
. Таким образом:
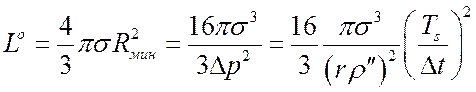 .
.
Чем больше перегрев Dt, тем меньше Lо.
Работа образования пузырька на теплоотдающей поверхности
будет несколько меньше (![]() ), т. к. паровой
пузырек кроме межфазной поверхности будет иметь поверхность раздела твердое
тело – жидкость, на которой молекулярное сцепление ослаблено. Поэтому
вероятность вскипания в этом случае выше.
), т. к. паровой
пузырек кроме межфазной поверхности будет иметь поверхность раздела твердое
тело – жидкость, на которой молекулярное сцепление ослаблено. Поэтому
вероятность вскипания в этом случае выше.
С учетом краевого угла кипения q можно записать:
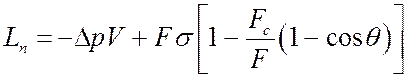 .
.
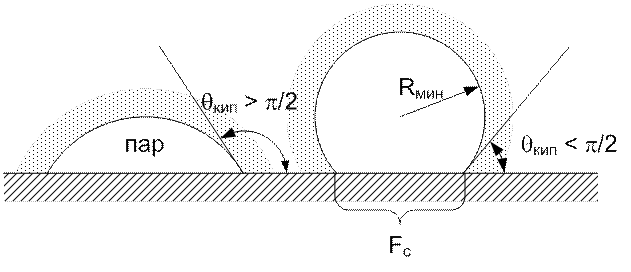
Рис. 78. Краевые углы кипения
При 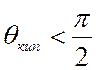 жидкость смачивает
поверхность, при
жидкость смачивает
поверхность, при 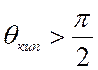 – не смачивает.
– не смачивает.
Отношение ![]() – доля поверхности
пузырька, на которой пар соприкасается с твердой поверхностью.
– доля поверхности
пузырька, на которой пар соприкасается с твердой поверхностью.
Из этого уравнения, чем больше ![]() и
значение q, тем работа Lп будет меньше. Наличие впадин, неровностей
как раз и обусловливает появление вскипания в этих местах. Локальные места
ухудшения смачиваемости также приводят к вероятному вскипанию (например,
загрязнения жирами – вспенивание водной поверхности при жировых включениях).
и
значение q, тем работа Lп будет меньше. Наличие впадин, неровностей
как раз и обусловливает появление вскипания в этих местах. Локальные места
ухудшения смачиваемости также приводят к вероятному вскипанию (например,
загрязнения жирами – вспенивание водной поверхности при жировых включениях).

Рис. 79. Образование пузырька во впадине
При ![]() происходит рост
паровых пузырьков за счет подвода тепла. Подвод тепла осуществляется путем
теплопроводности из окружающего пузырек перегретого слоя жидкости через
межфазную поверхность Fж и через поверхность
под пузырьком Fc в основании. Тепло
расходуется на испарение жидкости и работу расширения.
происходит рост
паровых пузырьков за счет подвода тепла. Подвод тепла осуществляется путем
теплопроводности из окружающего пузырек перегретого слоя жидкости через
межфазную поверхность Fж и через поверхность
под пузырьком Fc в основании. Тепло
расходуется на испарение жидкости и работу расширения.
На основании теории подобия получено критериальное уравнение теплообмена:
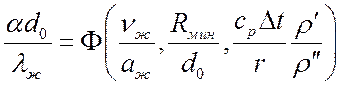 .
.
Интенсивность кипения определяет безразмерный комплекс этого уравнения, называемый числом Якоба:
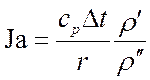 .
.
Оно показывает соотношение теплового потока, идущего на
нагрев единицы объема жидкости, и объемной теплотой парообразования ![]() .
.
С повышением давления число Ja уменьшается, т. к. увеличивается плотность пара r². С повышением перегрева жидкости число Ja возрастает, т. к. увеличивается Dt.
При повышенных давлениях (больше атмосферного) интенсивность роста пузырька выражается (при этом теплота передается в основном через основание Fc):
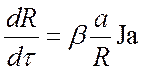 ,
,
где ![]() – постоянная;
– постоянная;
t – время;
a – коэффициент температуропроводности.
При низких давлениях насыщения:
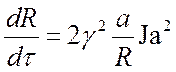 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.