Таким образом, закон Фурье формулируется: плотность теплового потока пропорциональна градиенту температуры.
Если градиент температуры для различных точек изотермической поверхности различен, то общий тепловой поток определится как
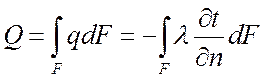, Вт,
где dF – элемент изотермической поверхности.
Полное количество тепла, прошедшее за время t через изотермическую поверхность F будет:
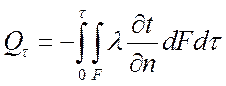, Дж.
Если удельный тепловой поток 
спроектировать
на координатные оси Ox, Oy, Oz, то получим:
,
,
.
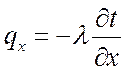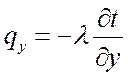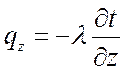Эти тепловые потоки являются составляющими вектора :
.
Для вычисления количества тепла, проходящего через поверхность твердого тела, необходимо знать температурное поле внутри тела. Нахождение температурного поля является задачей аналитической теории теплопроводности.
Коэффициент теплопроводности в общем случае зависит от температуры, давления и рода вещества.
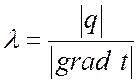, Вт/(м·K).
Коэффициент теплопроводности численно равен количеству тепла, проходящего в единицу времени через единицу изотермической поверхности при температурном градиенте, равном единице.
В большинстве случаев l определяется опытным путем.
l для твердых тел зависит от температуры, а для жидких и газов – от давления.
Для анизотропных тел l существенно зависит от направления передачи тепла. Так, для древесины l различается в 3 – 4 раза в зависимости от того, как передается тепло: вдоль волокон или поперек их. Например, для сосны l = 0,30 – 0,32 Вт/(м·K) (вдоль волокон), l = 0,14 – 0,16 Вт/(м·K) (поперек волокон).
Зависимость l от температуры для многих материалов в определенном диапазоне изменений температуры может быть определена по формуле:
,
где l0 – коэффициент теплопроводности при 0 °C;
b – опытный коэффициент;
t – температура, °C.
В соответствии с кинетической теорией газов перенос тепла теплопроводностью в газах при обычных давлениях и температурах определяется переносом кинетической энергии молекулярного движения в результате хаотического движения и столкновения отдельных молекул газа. Коэффициент теплопроводности определяется:
,
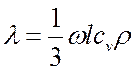где w – средняя скорость перемещения молекул газа;
l – средняя длина свободного пробега молекул газа между их столкновениями;
cv – теплоемкость газа при постоянном объеме;
r – плотность газа.
С увеличением давления уменьшается l, но увеличивается r, а произведение l·r сохраняется постоянным. Поэтому l для газов почти не зависит от давления. Исключение составляют слишком малые (менее 20 мм рт. ст.) и очень большие (более 2·104 бар) давления.
Средняя скорость движения молекул зависит от температуры:
,
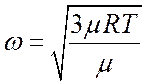где mR – универсальная газовая постоянная, равная 8314,2 Дж/(моль·K);
m – молекулярная масса газа, кг/моль;
T – температура, K.
Теплоемкость газов растет с повышением температуры, поэтому и l для газов с повышением температуры возрастает.
Для газов l = 0,006 – 0,6 Вт/(м·K). Наибольший l для водорода и гелия, он в 5 – 10 раз больше, чем у других газов. Меньший l у аргона.
Для водяного пара и других реальных газов l сильно зависит от давления.
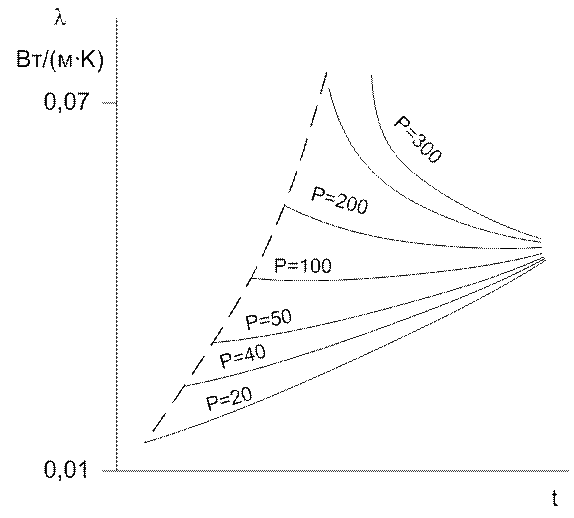
Рис. 3. Зависимость l пара от давления P
Для газовых смесей определить l по закону аддитивности нельзя, его нужно определять опытным путем.
Механизм распространения тепла в капельных жидкостях представляется как перенос энергии путем нестройных упругих колебаний.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.