Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 23

Аналитическое решение задачи является сложным, поэтому многие исследователи пренебрегают начальным режимом, а изучают только второй упорядоченный режим, подчиняющийся экспоненциальному закону. Этот режим Г. М. Кондратьев назвал регулярным.

Кроме того, в исследованиях применяют и экспериментальные методы, основанные на аналогии: между явлениями распространения тепла и ламинарного движения жидкости – метод гидротепловой аналогии [3], между тепловыми и электрическими процессами – метод электротепловой аналогии [4]. Многие сложные задачи нестационарной теплопроводности решаются с помощью ЭВМ.

Режим нестационарной теплопроводности при работе котлов не является основным, он проявляется только при пусках или остановах. А вот в работе нагревательных печей этот режим является основным, т. к. качество продукции зависит от режима нагрева заготовок, и поэтому необходимо проводить расчет режима.

4.2. Аналитическое решение процесса

Для твердых тел нестационарный режим описывается дифференциальным уравнением:

                                               .

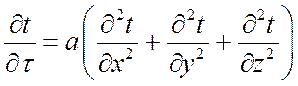Для решения уравнения задаются краевые условия:

1) начальные – начальное распределение температуры в теле;

2) граничные условия – I, II, III рода.

а) при граничных условиях I рода задается температура поверхности t_c, что графически выражается заданием точки A, но количество тепла dQ, проходящее через элемент поверхности dF, при этом неизвестно. Следовательно, неизвестен угол наклона температурной кривой в теле около поверхности, т. е. угол 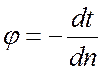, ибо по закону Фурье для любого момента времени количество тепла, приходящее изнутри тела к поверхности, равно:

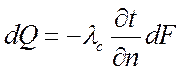                                                    , Вт.

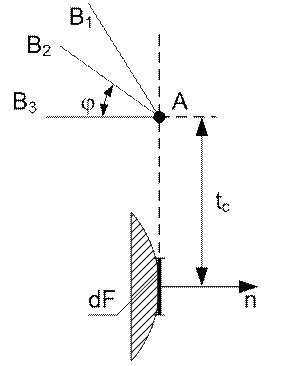
Рис. 34. Граничные условия I рода

б) при граничных условиях II рода задается количество тепла, проходящего через поверхность dF (т. е. в конечном счете угол j), но неизвестна ордината t_c, т. е. положение точки A.

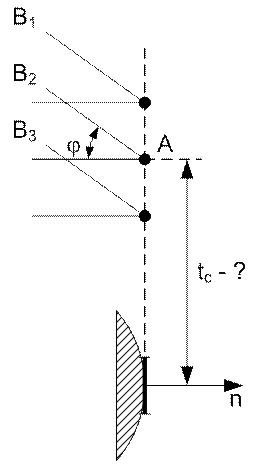
Рис. 35. Граничные условия II рода

в) при граничных условиях III рода задается температура окружающей среды tж и коэффициент теплоотдачи a в окружающую среду. Записав баланс тепловой энергии, притекающей изнутри тела к поверхности и отданной за счет теплоотдачи, получим:

                                               ,

                                                     .

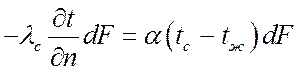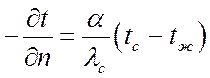Это математическая формулировка граничного условия III рода.

Из рисунка получим:

                                        ,

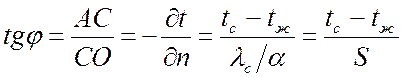где 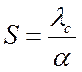  , м.

Таким образом, условием III рода определяется точка O, через которую должны проходить все касательные к температурной кривой в точке, лежащей на поверхности тела (в конкретном случае в точке A). Точка O называется направляющей, и лежит на расстоянии 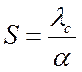 от поверхности. Отрезок S является подкасательной к температурной кривой, от формы поверхности она не зависит, размерность – м.

Решить уравнение нестационарной теплопроводности – значит найти такую функцию, которая одновременно удовлетворяла бы этому уравнению и краевым условиям. Решение уравнения производится при помощи рядов Фурье. Для различных граничных условий результаты решения получаются различными, но методология примерно одинакова. Для технических целей в большинстве случаев можно ограничиться рассмотрением процесса лишь в одном направлении, например, по оси x. Тогда общее решение имеет вид:

плоская стенка:

                                ;

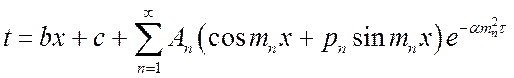цилиндрическая стенка:

                          ,

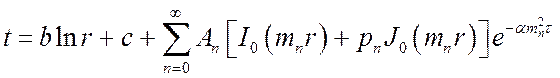где   I₀ и J₀ – бесселевы функции первого и второго рода.

Постоянные b и c определяются из условий стационарного режима (при ), p_n и m_n – из граничных и A_n – из начальных (при ) условий.

Из приведенных решений следует, что искомая функция зависит от большого числа параметров. Однако из анализа решений оказывается, что эти величины можно сгруппировать в два безразмерных комплекса:  и , которые являются критериями подобия:

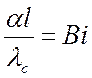                                                 – критерий Био;

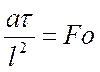                                              – критерий Фурье.