Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 41

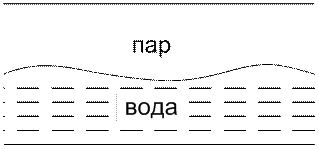
Пузырьковый режим отвода тепла является самым совершенным методом охлаждения поверхностей нагрева, широко применяется в атомных реакторах, при охлаждении реактивных двигателей. В котлах при пузырьковом кипении происходит процесс генерации пара и отвод тепла от стенок труб, находящихся в раскаленном газовом потоке.

Условия кипения в ограниченном объеме (двигающийся поток жидкости в трубе) такие же, но появляется ряд новых особенностей:

1) на развитие процесса влияет скорость вынужденного движения потока жидкости в трубе;

2) важное значение имеет характер распределения паровой и жидкой фаз в пароводяном потоке.

                                 г)                                                                  д)

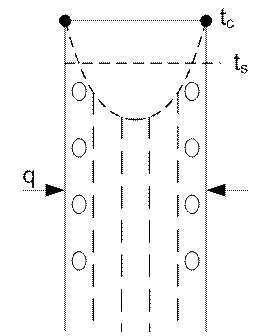
Рис. 77. Кипение в ограниченном объеме

а – однородная смесь (пар – вода);

б – два самостоятельных потока: вода – около стенки, пар – в центральной части;
в – пузырьковый режим;

г – раздельное движение;

д – недогретая жидкость.

7.1.2. Пузырьковый режим кипения

Опыт показывает, что при увеличении , а также давления p на поверхности увеличивается число активных центров парообразования z, увеличивается число пузырьков, растет турбулизация жидкости и съем тепла, кипение носит хаотичный характер. Число z зависит от шероховатости материала, неоднородности поверхности и наличия адсорбированного на поверхности воздуха.

Под работой адгезии понимают работу, затрачиваемую для отрыва жидкости от твердой поверхности на единицу площади, она характеризует меру молекулярного сцепления и связана с явлением смачивания. Чем лучше жидкость смачивает участок поверхности, тем выше работа адгезии.

Газ, растворенный в жидкости, постепенно уносится в пар, кипение приобретает стабильный характер.

На условия парообразования оказывает влияние поверхностное натяжение на границе раздела жидкости и пара.

Поверхностным натяжением называется сила, под действием которой свободная поверхность жидкости стремится сократиться, она действует по касательной к поверхности. Обозначается s, Н/м, и является характеристикой жидкости (при 20 °C: вода – 0,068, бензол – 0,0288, этиловый спирт – 0,0222, ртуть – 0,47). С увеличение температуры s убывает, и при t_кр равна нулю.

По формуле Бачинского:

                                                       ,

где   C – коэффициент пропорциональности.

Вследствие поверхностного натяжения давление пара внутри пузырька p_п выше давления жидкости p_ж. По формуле Лапласа уравнение равновесия:

                                                    ,

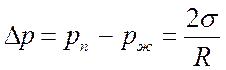где   R – радиус пузырька (средний радиус кривизны поверхности раздела жидкости и пара). Чем меньше R, тем больше Dp.

Для существования теплового равновесия жидкость, окружающая пузырек, должна быть перегрета на величину , т. к. пар в пузырьке и жидкость на его поверхности находятся в равновесии, если поверхность жидкости имеет температуру, равную температуре насыщения при давлении пара в пузырьке – . Это равновесие оказывается неустойчивым, если температура жидкости несколько превысит равновесное значение – произойдет испарение жидкости внутрь пузырька, его радиус увеличится, и по уравнению Лапласа давление пара p_п в пузырьке понизится. Это приведет к новому отклонению от равновесного состояния. Пузырек начнет неограниченно расти. И наоборот: при понижении температуры жидкости часть пара сконденсируется, радиус пузырька уменьшится, давление в нем повысится. В итоге пузырек сконденсируется и исчезнет.

Минимальное значение радиуса пузырька R_мин называется критическим. Выше этого значения пузырьки способны к дальнейшему росту. R_мин зависит от степени перегрева жидкости , где t_s – температура насыщения при давлении в жидкости. По формуле Лапласа:

                                                            ,

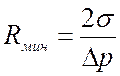где   Dp – разность давлений между паром и жидкостью:

                                          ;