Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 25

Обозначим множители ряда 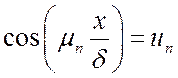, 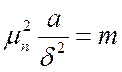. Тогда в стадии регулярного режима процесс описывается первым членом ряда:

                                                          ,                       (*)

из которого видно, что q не зависит от начального распределения температур.

Логарифмирование выражения (*) при опускании индексов дает:

                            , или .                                                                  (**)

На графике стадия регулярного режима описывается прямой линией.

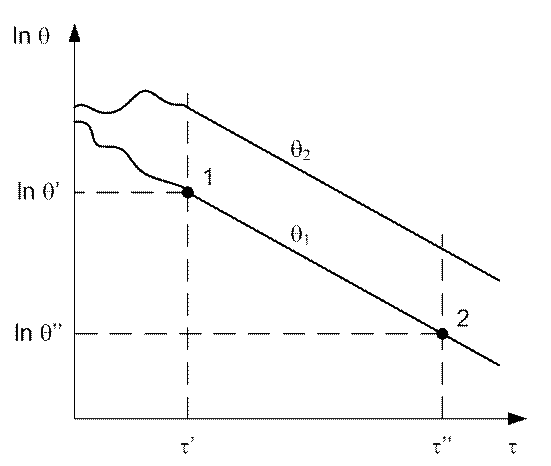
Рис. 38. График регулярного режима

Если продифференцировать выражение (**), то получим:

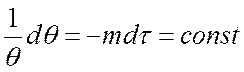                                     , или .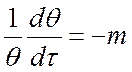

В левой части уравнения – относительная скорость изменения температуры, она равна постоянному значению и не зависит ни от координат, ни от времени.

Величина m, 1/с, характеризует интенсивность охлаждения тела и называется темпом охлаждения (нагревания). Темп охлаждения можно подсчитать как:

                                                       .

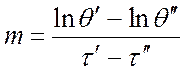Особенности:

1) Темп охлаждения однородного тела m при конечном значении коэффициента теплоотдачи пропорционален коэффициенту теплоотдачи a и внешней поверхности тела F и обратно пропорционален полной теплоемкости тела :

                                                            .

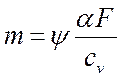2) Основное соотношение , определяющее наступление регулярного режима, выполняется не только для однородных простых тел, но и для любых сложных систем из разнородных тел, т. е. явление регуляризации температурного поля имеет общий характер.

3) При  значение m_¥ для любой сложной системы конечно, при чем величина m_¥ для однородных тел пропорциональна коэффициенту температуропроводности a материала:

                                                              .

Выражение 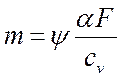 есть формула закона сохранения энергии для условий регулярного режима охлаждения (нагревания) тела. Величина 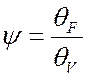 есть отношение средней по поверхности избыточной температуры q_F к средней ее величине по объему тела q_V. y остается постоянной в течение всего регулярного режима. Диапазон принимаемых значений: . При  имеем равномерное поле температур в теле.

Коэффициент k имеет размерность м² и зависит от геометрических свойств: формы и размеров тела. Он называется коэффициентом формы тела. Для тел простой формы k можно подсчитать по формулам:

                                                    для шара: ;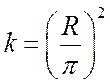

                             для цилиндра длиной l: ;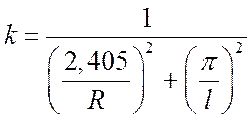

                                для параллелепипеда со сторонами l₁, l₂, l₃: .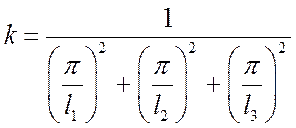

Для тел сложной формы k определяется опытным путем. С этой целью из материала с известным коэффициентом температуропроводности изготовляется модель, геометрически подобная объекту сложной формы. Экспериментальным путем для модели определяется темп охлаждения m_¥ в условиях высокой интенсивности теплоотдачи () и из соотношения  определяется k_мод. Тогда коэффициент формы для тела 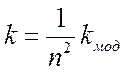, где n – отношение линейных размеров модели и объекта.

Выражение  есть предельный случай уравнения 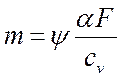 при  и , а качественный характер зависимости  показан на рис.

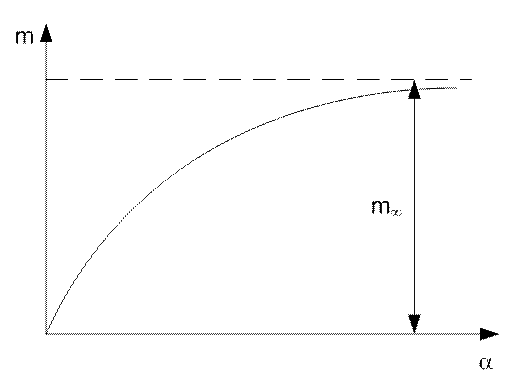
Рис. 39. График

Подставив в относительный темп охлаждения

                                                        

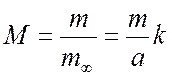
модифицированную форму записи критерия Био

                                                            ,

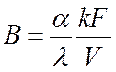получим:

                                                             .

Величина y есть однозначная функция критерия B для тела заданной формы. Для тел различной конфигурации эту зависимость можно выразить кривой, описывающей семейство близко располагающихся друг к другу кривых:

                                                 .

5. Конвективный теплообмен в однородной среде

5.1. Основные понятия и определения

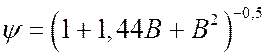Конвективным теплообменом, или теплоотдачей, называется процесс переноса тепла между поверхностью твердого тела и жидкой (подвижной) средой. При этом перенос тепла осуществляется одновременным действием теплопроводности и конвекции.