Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 6

Эта теория выдвинута русским ученым А. С. Предводителевым. По этой теории:

                                            , ,

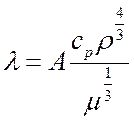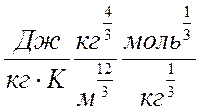где   c_p – изобарная теплоемкость;

        r – объемная плотность жидкости;

        m – молекулярная масса.

Коэффициент A, пропорциональный скорости распространения упругих волн в жидкости, не зависит от природы жидкости, но зависит от температуры, при этом .

Т. к. для неассоциированных жидкостей их плотность с повышением температуры убывает, то и l их также убывает (вазелиновое масло, бензол, ацетон, касторовое масло, этиловый спирт и др.). Однако для ассоциированных жидкостей (вода, спирт) это следует учесть коэффициентом ассоциации, который зависит от температуры и может влиять на l по разному. Например, для воды и глицерина с ростом температуры l увеличивается.

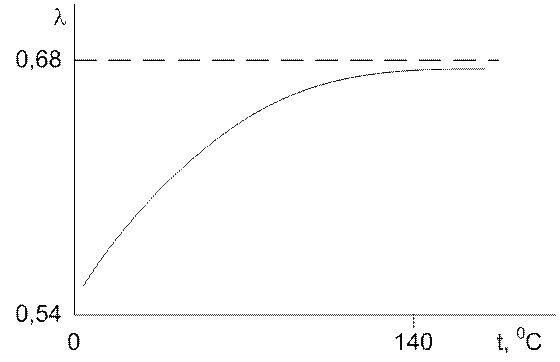
Рис 4. Зависимость l от температуры для воды

Для капельных жидкостей l = 0,07 – 0,7 Вт/(м·K). При повышении давления l для жидкостей возрастает.

2.4.3. Коэффициент теплопроводности твердых тел

2.4.3.1. Металлы и сплавы

В металлах основным передатчиком тепла являются свободные электроны, которые можно уподобить идеальному одноатомному газу. Передача тепла здесь идет электронным газом. При повышении температуры из-за наличия неоднородностей и рассеяния электронов l чистых металлов снижается, особенно у Ni. При наличии примесей коэффициент теплопроводности металлов резко убывает. Чистая медь: l = 396 Вт/(м·K), медь с примесью мышьяка: l = 142 Вт/(м·K).

Коэффициент теплопроводности металлов лежит в пределах l = 20 – 400 Вт/(м·K).

Таблица 1

Металл	l, Вт/(м·K)
Ag	410
Cu	395
Au	300
Al	210
Сталь, C = 0,1 %	49
Сталь, C = 1,0 %	40
Сталь, C = 1,5 %	36

В отличие от чистых металлов, l сплавов с ростом температуры увеличивается.

2.4.3.2. Диэлектрики (неметаллы)

В диэлектриках с повышением температуры l обычно увеличивается. Для материалов с большей объемной плотностью l имеет более высокие значения. Пористые материалы (порошки) имеют l сильно зависящим от объемной плотности r. С возрастанием плотности возрастает l пористых материалов.

Для влажных пористых материалов l больше, чем для воды и сухого материала. Это объясняется возникновением конвективного переноса тепла в капиллярах наряду с теплопроводностью.

Для строительных и теплоизоляционных материалов l находится в пределах l = 0,023 – 2,9 Вт/(м·K).

Материалы с l < 0,25 Вт/(м·K) называются теплоизоляционными.

2.5. Дифференциальное уравнение теплопроводности

Распределение температуры в теле описывается дифференциальным уравнением теплопроводности.

При выводе дифференциального уравнения сделаем ряд допущений.

1. Рассматриваемое тело однородно и изотропно.

2. Температурные деформации рассматриваемого элементарного объема dV малы по сравнению с самим объемом тела.

3. Внутренние источники тепла в теле (которые могут быть заданы как ) распределены равномерно.

4. Макроскопические частицы тела неподвижны относительно друг друга.

5. Физические параметры тела постоянны во времени и пространстве.

Выделим элементарный объем с гранями dx, dy, dz.

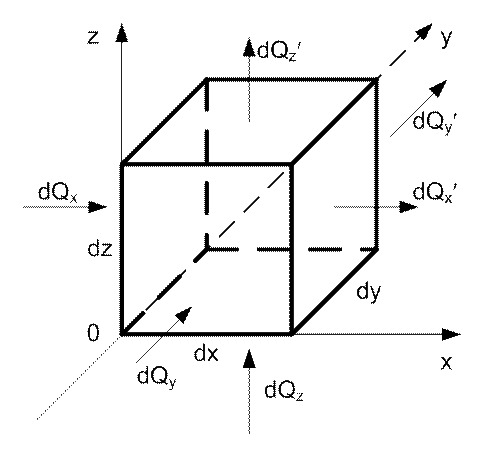
Рис. 5. Элементарный объем

Подведем к элементарному объему dV количество тепла dQ₁ за время dt. Предположим, что за это же время за счет внутренних источников тепла выделилось тепла в теле dQ₂. Тогда на основе закона сохранения энергии можно записать:

                                                        ,

где   dQ – суммарное изменение внутренней энергии тела в объеме dV за время dt.

Обозначим количество тепла, подводимого к граням dV за время dt в направлении Ox, Oy, Oz: dQ_x, dQ_y, dQ_z. Количество тепла, отводимого через противоположные грани в тех же направлениях: , , .

Разница между подведенным и отведенным количествами тепла в направлении осей x, y, z за время dt может быть представлена в виде:

                                                       ,