По аналогии с понятиями гидродинамического и теплового пограничного слоя можно представить наличие диффузионного пограничного слоя толщиной dдифф. В его пределах концентрация активного компонента смеси изменяется от mi.с на поверхности раздела фаз до mi.0 на внешней границе слоя.
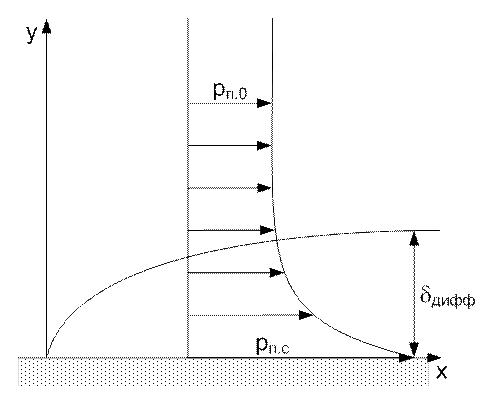
Рис. 90. Диффузионный пограничный слой
Внутри пограничного слоя:
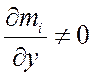 ,
,
а вне диффузионного пограничного слоя выполняется условие:
![]() ;
; 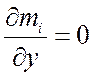 .
.
Диффузионный пограничный слой может наблюдаться в процессах испарения, сублимации, вдува вещества через пористую стенку, при конденсации пара из парогазовой смеси и т. д.
В случае продольного омывания плоской неограниченной пластины поле концентраций в диффузионном пограничном слое описывается дифференциальным уравнением:
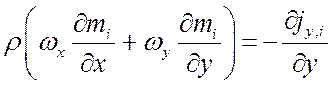 ,
,
где jy,i – поперечная составляющая плотности потока массы i-го компонента смеси.
Для турбулентного переноса массы в пограничном диффузионном слое:
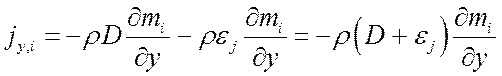 ,
,
где ej – коэффициент турбулентного переноса вещества, м2/с.
Здесь wx, wy, wz, jx,i, jy,i – осредненные во времени величины.
Представленное уравнение справедливо при условии, что ![]() , т. е. поперечная составляющая скорости
около поверхности, обусловленная процессом испарения, должна быть намного
меньше скорости вынужденного продольного движения w0. Если же
, т. е. поперечная составляющая скорости
около поверхности, обусловленная процессом испарения, должна быть намного
меньше скорости вынужденного продольного движения w0. Если же ![]() , то
преобладает движение по нормали к поверхности, и продольное движение
несущественно.
, то
преобладает движение по нормали к поверхности, и продольное движение
несущественно.
Проследим аналогию для процессов теплообмена и массообмена
для стационарных процессов продольного ламинарного омывания плоской пластины.
Скорости считаем умеренными, физические параметры в пограничных слоях
постоянными, 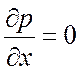 .
.
Для теплообмена уравнения энергии, движения и сплошности
для простейших граничных условий (![]() ):
):
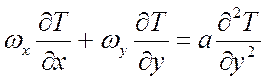 ;
;
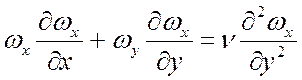 ;
;
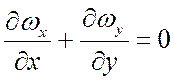 ;
;
при ![]() :
: ![]() ,
, ![]() ,
, ![]() ;
;
при ![]() :
: ![]() ,
, ![]() .
.
В случае массообмена считаем, что стенка проницаема для одного из компонентов. Течение изотермическое. Граничные условия в основном не отличаются от приведенных условий. Тогда для массообмена:
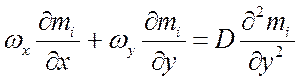 ;
;
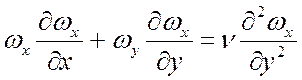 ;
;
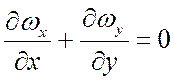 ;
;
при ![]() :
: ![]() ,
, ![]() ,
, ![]() ;
;
при ![]() :
: ![]() ,
, ![]() .
.
Сравнивая приведенные математические формулировки,
наблюдаем почти полную аналогию за исключением того, что для тепловой задачи в
силу непроницаемости стенки задано для точки с координатами ![]()
![]() , а в
случае массообмена имеем
, а в
случае массообмена имеем ![]() – поперечную
составляющую wy,c,
которая может быть в общем случае заданной функцией x.
– поперечную
составляющую wy,c,
которая может быть в общем случае заданной функцией x.
Если положить ![]() , то решение задач
теплообмена и массообмена будут совпадать полностью. В противном случае решение
задачи сводится к решению аналогичной задачи, но с измененными начальными
условиями: либо
, то решение задач
теплообмена и массообмена будут совпадать полностью. В противном случае решение
задачи сводится к решению аналогичной задачи, но с измененными начальными
условиями: либо ![]() , либо
, либо ![]() .
Последний фактор совсем исключается, если поля температур и концентраций представлять
в безразмерном виде. Тогда получается полное совпадение задач, причем
.
Последний фактор совсем исключается, если поля температур и концентраций представлять
в безразмерном виде. Тогда получается полное совпадение задач, причем ![]() (отношение
(отношение 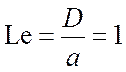 –
число Льюиса-Семенова).
–
число Льюиса-Семенова).
Аналогия процессов тепло- и массообмена часто используется на практике. Например, если известно критериальное уравнение теплообмена в виде:
![]() ,
,
то по аналогии полагают, что при массообмене:
![]() ,
,
где функции j и y одинаковы;
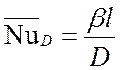 – диффузионное число Нуссельта;
– диффузионное число Нуссельта;
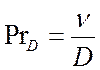 – диффузионное число Прандтля.
– диффузионное число Прандтля.
![]() и PrD
– аналоги
и PrD
– аналоги ![]() и Pr.
и Pr.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.