Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 20

Для цилиндра, как и для пластины, задача будет одномерной и симметричной. Дифференциальное уравнение имеет вид:

                                                    .

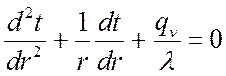Граничные условия:

                                                  при  ;

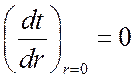                                         при  ,

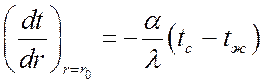т. к. , и по закону Фурье .

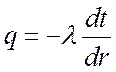Определить: уравнение температурного поля, тепловой поток и температуры на оси t₀ и на поверхности t_c.

Имеем дифференциальное уравнение:

                                                    .

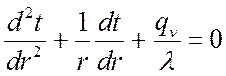Обозначим 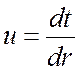 и заменим, получим:

                                                       .

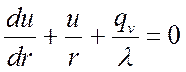Представим , тогда :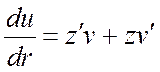

                                                    ,

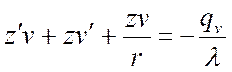или

                                                   .

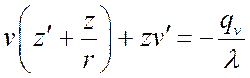Найдем функцию, чтобы :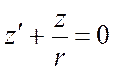

                            1) , , , .

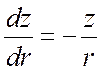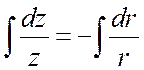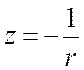         2) , , , ,

                                            ,

                                                       .                   (*)

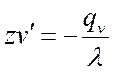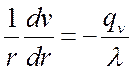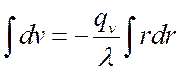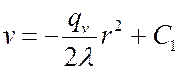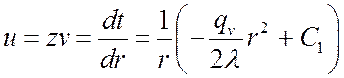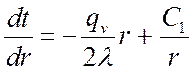Интегрируем второй раз:

                                                ,

                                                 .           (**)

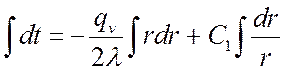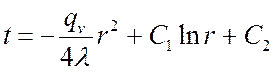Из (*):

                                при  ;

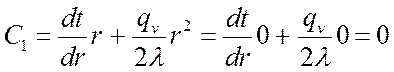                            при  , .

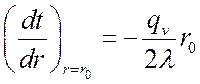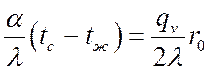Из (**) определим C₂:

                    ,

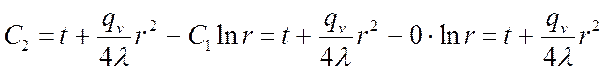но при  , тогда:

                                                        .

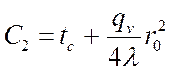Подставив полученное выражение в (**), получим:

                                   .

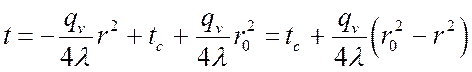Т. к. 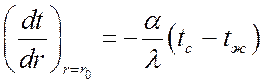, получим:

                                                         .

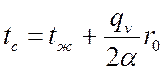Тогда температурное поле описывается уравнением:

                                             .

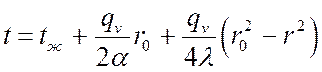Это уравнение параболы. Из этого уравнения:

                                                  .

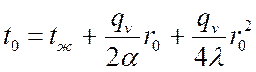Удельный тепловой поток:

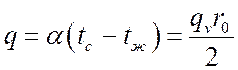                                              , Вт/м².

Полный поток с поверхности цилиндра:

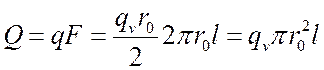                                          , Вт.

Если положить , то  при сильном охлаждении, тогда:

                                                 ,

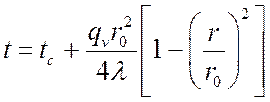а температура на оси цилиндра при :

                                                          .

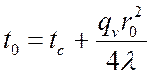Если учитывать зависимость l от температуры: , то:

                                              .

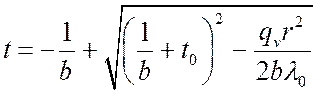Резюме: плотность теплового потока зависит только от теплопроизводительности внутренних источников и от величины внешней поверхности (r₀), через которую проходит тепловой поток. Температура изменяется по закону параболы.

3.9.3. Теплопроводность цилиндрической стенки

Имеем бесконечно длинную цилиндрическую трубу с внутренним радиусом r₁, наружным r₂ и постоянным коэффициентом теплопроводности l. Внутри стенки трубы имеются равномерно распределенные источники тепла с производительностью q_v.

В такой стенке температура будет изменяться только в направлении радиуса, и процесс описывается уравнением:

                                                    .

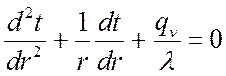После интегрирования:

                                                  ,

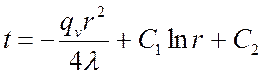где   C₁ и C₂ – постоянные интегрирования, определяемые из граничных условий.

3.9.3.1. Тепло отводится только через наружную поверхность трубы

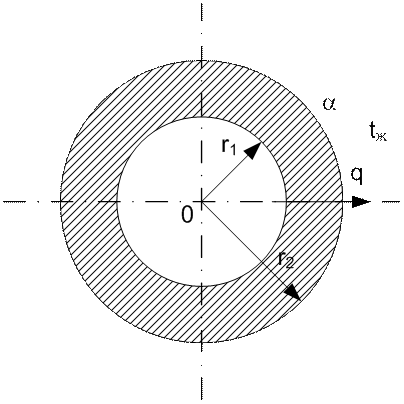
Рис. 28. Теплоотвод через наружную поверхность трубы

Заданы граничные условия третьего рода:

                                             при   ;

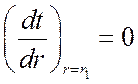                                        при  .

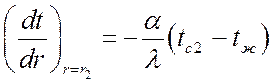Из 3.8.2 имеем после решения дифференциального уравнения:

                                          , .

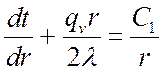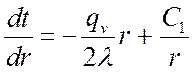При  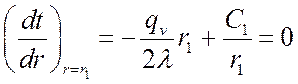. Отсюда:

                                                            .

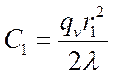При   .

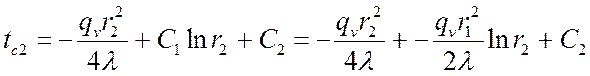Из граничных условий находим:

                 ,

                                              .

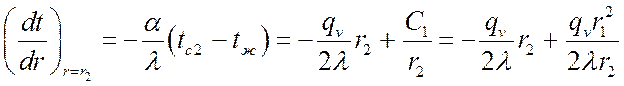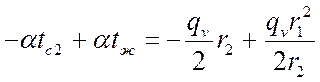Отсюда:

                                                  .

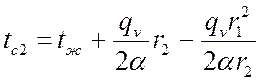Тогда:

                                   .

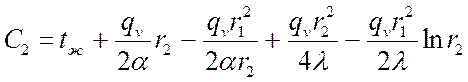Подставляя значения C₁ и C₂ в решение дифференциального уравнения, получим:

        

                .

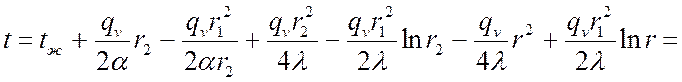
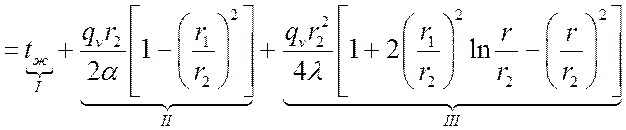Для внешней теплоотдающей поверхности ():

                                                ,

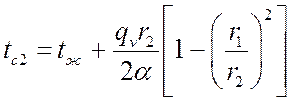третье слагаемое обращается в нуль.

Удельный тепловой поток с единицы теплоотдающей поверхности:

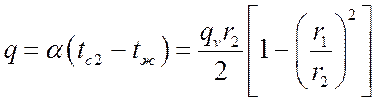                                    , Вт/м².

Температура на внутренней поверхности стенки ():