Если теплоотдачей с конца стержня пренебречь, то граничные условия запишутся:
б) при ![]()
![]() ;
;
при ![]()
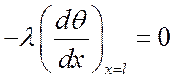 , т.
е.
, т.
е. ![]() .
.
Подставим эти граничные условия в уравнение ![]() и вычислим C1
и C2:
и вычислим C1
и C2:
а) при ![]()
![]() , т. к.
, т. к.
![]() ;
;
при ![]()
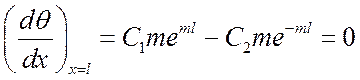 .
.
Тогда:
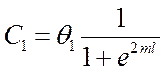 ,
,
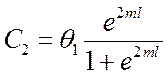 .
.
Отсюда:
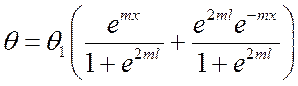 ,
,
или, если умножить и разделить правую часть на ![]() , то получим:
, то получим:
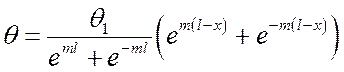 .
.
Но известно, что 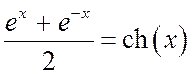 ,
, 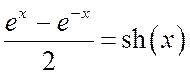 . Тогда:
. Тогда:
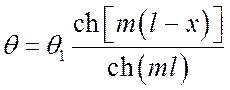 , °C. (*)
, °C. (*)
По этой формуле можно вычислить температуру в любом
сечении стержня. В предельном случае, когда ![]() :
:
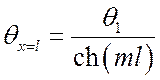 , °C,
, °C,
т. к. ![]() .
.
В том случае, когда теплоотдачей с конца стенки пренебречь нельзя, тогда решение ведется при граничных условиях а). После вычисления постоянных интегрирования C1 и C2 получим:
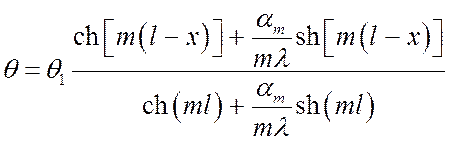 , °C. (**)
, °C. (**)
Последнее уравнение при 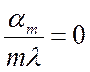 приходит
в предыдущее (*), следовательно, решение (*) есть частный случай общего решения
(**).
приходит
в предыдущее (*), следовательно, решение (*) есть частный случай общего решения
(**).
Количество тепла, передаваемое стержнем (ребром) через основание:
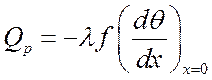 .
.
Из (*) находим:
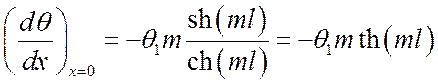 ,
,
т. к. 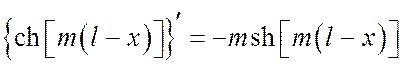 .
.
Тогда:
![]() , Вт.
, Вт.
Подставим 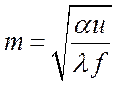 , получим:
, получим:
![]() . (***)
. (***)
Если длина стержня очень велика, то ![]() , а
, а ![]() , и
следовательно:
, и
следовательно:
![]() ,
, ![]() .
.
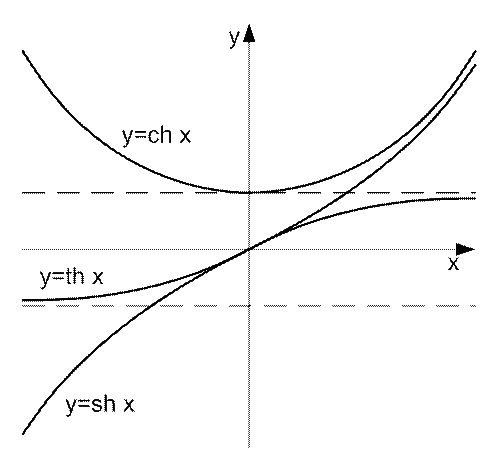
Рис. 23. Гиперболические тригонометрические функции
th 3 = 0,995; th 4 = 0,999
Рассмотрим плоскую ребристую стенку безграничных размеров. Стенка оребрена со стороны меньшего коэффициента теплоотдачи.

Рис. 24. Ребристая плоская стенка
Задано: a1 – коэффициент теплоотдачи со стороны гладкой поверхности; aс – коэффициент теплоотдачи гладкой части оребренной поверхности; aр – коэффициент теплоотдачи ребер; tж1 и tж2 – температуры теплоносителей.
Поскольку ![]() , то можно принять
периметр
, то можно принять
периметр ![]() . Площадь сечения
. Площадь сечения ![]() .
Тогда:
.
Тогда:
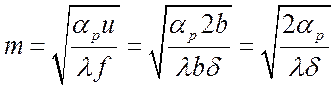 ,
1/м.
,
1/м.
Подставив в уравнение (***) и умножив и разделив на ![]() , получим:
, получим:
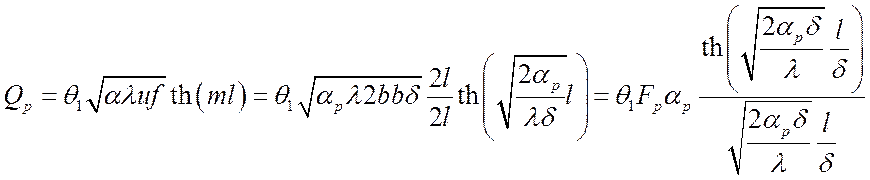 ,
,
где ![]() – площадь поверхности ребра.
– площадь поверхности ребра.
Отношение 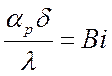 – безразмерный
критерий Био. Он представляет собой отношение внутреннего термического
сопротивления теплопроводности к внешнему термическому сопротивлению
теплоотдачи:
– безразмерный
критерий Био. Он представляет собой отношение внутреннего термического
сопротивления теплопроводности к внешнему термическому сопротивлению
теплоотдачи:
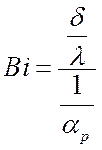 .
.
Окончательно тепловой поток с поверхности ребра:
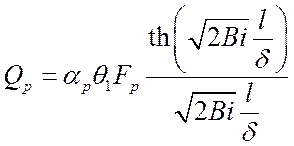 ,
Вт.
,
Вт.
Обозначим:
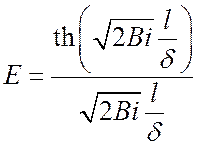 – коэффициент эффективности
ребра.
– коэффициент эффективности
ребра.
Тогда тепловой поток с поверхности ребра:
![]() , Вт.
, Вт.
Коэффициент эффективности 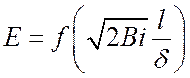 принимает
максимальное значение, равное 1, при
принимает
максимальное значение, равное 1, при 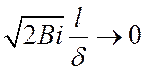 , что возможно при
заданных размерах ребра в случае, если
, что возможно при
заданных размерах ребра в случае, если ![]() , т. е.
при
, т. е.
при ![]() .
.
Тепло, отдаваемое гладкой частью оребренной поверхности:
![]() , Вт.
, Вт.
Общее количество тепла:
![]() ,
,
или
![]() ,
,
где 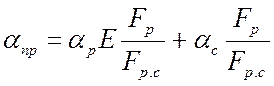 – приведенный коэффициент
теплоотдачи – это некоторый усредненный коэффициент теплоотдачи ребристой
стенки, который учитывает теплоотдачу поверхности ребра, гладкой части стенки и
эффективность работы ребра;
– приведенный коэффициент
теплоотдачи – это некоторый усредненный коэффициент теплоотдачи ребристой
стенки, который учитывает теплоотдачу поверхности ребра, гладкой части стенки и
эффективность работы ребра;
Fр.с – поверхность ребристой стенки;
Fр – поверхность ребра;
Fс – поверхность гладкой части ребристой стенки.
Для ребристой стенки запишем:
![]() ,
,
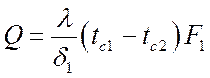 ,
,
![]() .
.
Отсюда:
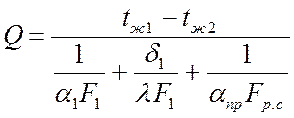 ,
Вт.
,
Вт.
Удельный тепловой поток через рабочую стенку:
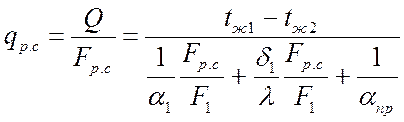 ,
Вт/м2.
,
Вт/м2.
или
![]() ,
,
где
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.