Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 7

                                                      ,

                                                       .

Если q_x, q_y, q_z – проекции плотности теплового потока на направление нормали к граням zy, zx, xy, тогда:

                                              ,

                                              ,

                                              .

Функции , ,  являются непрерывными в рассматриваемом диапазоне dx, dy, dz и могут быть разложены в ряд Тейлора:

                                           ,

                                          ,

                                           .

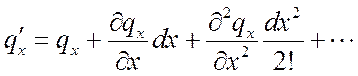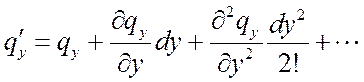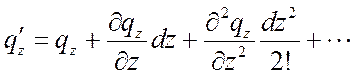Если ограничиться двумя первыми членами, то система с DQ может быть переписана:

                                                  ,

                                                  ,

                                                  .

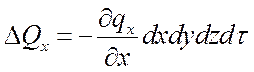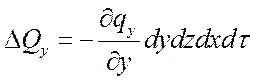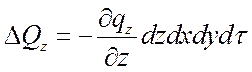Тогда суммарное количество тепла, подведенного к элементарному объему dV за время dt составит:

               .

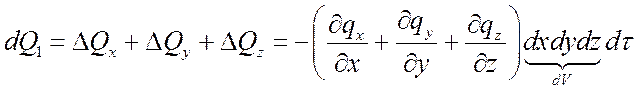Количество тепла, выделившееся за счет внутренних источников тепла, составит:

                                              .

Изменение внутренней энергии тела элементарного объема за время dt вследствие подвода тепла dQ₁ и dQ₂ выразим уравнением теплового баланса:

                                                      ,

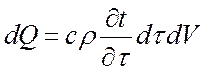где   c – теплоемкость тела;

        r – плотность вещества тела.

Подставим выражения dQ, dQ₁, dQ₂ в формулу теплового баланса:

                                                        ,

                  .

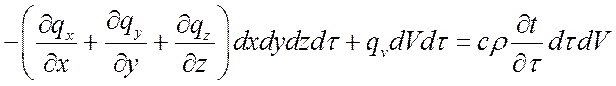После преобразования получим:

                                        .

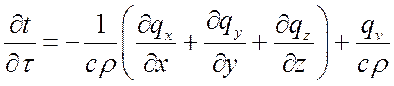По закону Фурье можно записать:

                                       ; ; .

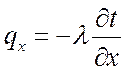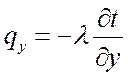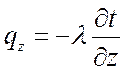Тогда, произведя замену, получим:

                                          .

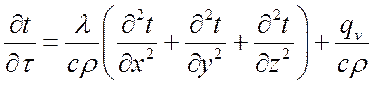Обозначим:

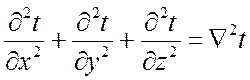 – оператор Лапласа.

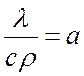, м²/с – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, в которой происходит процесс теплопроводности.

В окончательном виде:

                                                       .

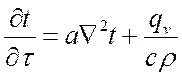Это уравнение называется дифференциальным уравнением теплопроводности. Оно устанавливает связь между временным и пространственным изменением температуры в любой точке тела, в которой происходит процесс теплопроводности.

В цилиндрических координатах это уравнение имеет вид:

                                   .

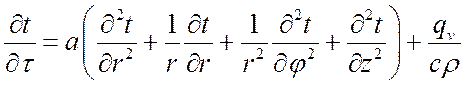Коэффициент температуропроводности важен для нестационарных процессов теплопроводности. Если коэффициент теплопроводности l характеризует способность тел проводить тепло, то коэффициент температуропроводности a характеризует меру теплоинерционных свойств тела. Как следует из дифференциального уравнения, скорость изменения температуры  тем больше, чем больше коэффициент температуропроводности a. Величина a зависит от природы вещества. Жидкости и газы обладают малым a – они инерционны; металлы, наоборот, обладают меньшей тепловой инерцией и, следовательно, большим a.

Таблица 2

Вещество	Температура, °C	a, м2/с
Сухой воздух	0	18,8·10–6
	20	21,4·10–6
Вода на линии насыщения	0	13,2·10–6
	20	14,3·10–6
	100	16,8·10–6
Cu	0	114,5·10–6
Al	0	91,3·10–6
Сталь	20	12,5·10–6

2.6. Условия однозначности для процессов теплопроводности

Дифференциальные уравнения, как правило, выводят на основе общих законов физики, и поэтому могут иметь бесконечное множество решений.

В конкретном случае для полного математического описания процесса теплопроводности необходимо внести частные особенности рассматриваемого процесса. Эти частные особенности называют условиями однозначности или краевыми условиями. Они включают в себя:

а) геометрические условия (форма, размеры тела, в котором протекает процесс);

б) физические условия (физические свойства тела и его физические параметры);