Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 27

Он представляет относительное изменение объема при изменении температуры на 1 K при . Для жидкостей b сравнительно мал. Для воды при  °C b может иметь отрицательное значение. Для газов:

                                                               .

5.2. Дифференциальные уравнения конвективного теплообмена

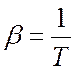Из уравнения 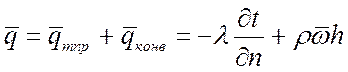 следует, что плотность теплового потока в любой точке жидкости для каждого момента времени однозначно определяется, если известны поля температур, энтальпии и скорости.

Связь между энтальпией и температурой для реальной жидкости , и согласно понятию о полном дифференциале:

                                              ,

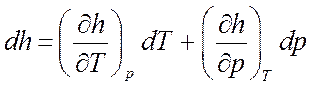тогда

                                                 .

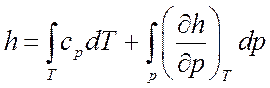Из термодинамики известно, что:

                                    .

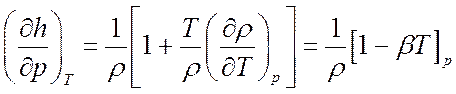Для многих задач для несжимаемых жидкостей () можно принять в приближении 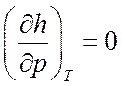, т. е. воспользоваться выражением для идеального газа:

                                                  , .

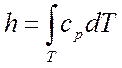Эти уравнения устанавливают связь между полем температур и полем энтальпии. Зная одно, можно определить другое. Таким образом, чтобы найти поле температур (энтальпии) и поле скорости, и определить , необходимы следующие уравнения.

5.2.1. Уравнение энергии

В п. 2.5 было получено уравнение теплопроводности:

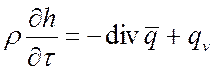         , или ,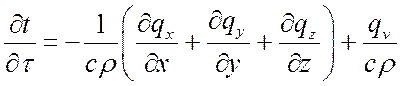

где   ;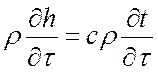

        ;

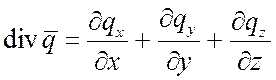        q_v – теплота внутренних источников.

Учитывая, что при конвективном теплообмене имеет место теплопроводность и конвекция, проекции теплового потока на координатные оси Ox, Oy, Oz будут:

          ; ; .

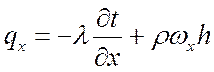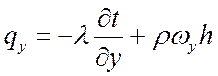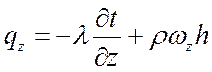С учетом этого получим:

          

                                             .

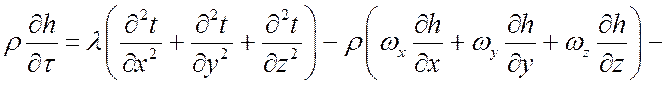
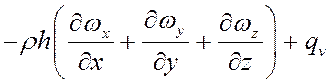Для несжимаемых жидкостей  и

                                             ,

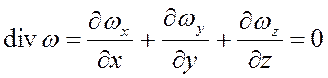тогда

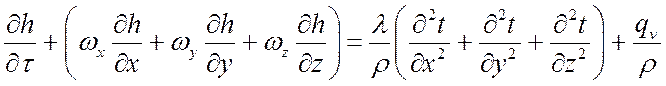           .                                                                   (1)

Если 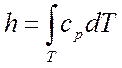 (для идеальных газов), то:

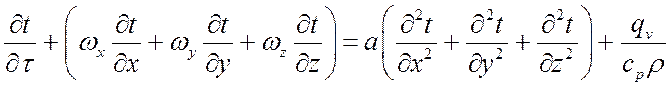          .                                                                   (2)

Уравнения (1) и (2) представляют собой искомые уравнения энергии, описывающие распределение температуры внутри движущейся жидкости.

В левой части уравнения (2) имеем полную производную от температуры по времени:

                                          ,

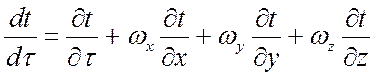в которой  – локальное изменение температуры по времени в какой-либо точке жидкости, а 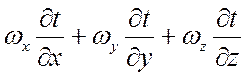 характеризует изменение температуры при переходе от точки к точке, т. е. конвективным изменением t.

Таким образом, применяя обозначение:

                                                  ,

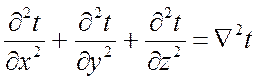уравнение энергии можно записать:

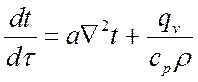                                                      .                   (3)

Если , уравнение переходит в уравнение теплопроводности, т. е.:

                                                      .

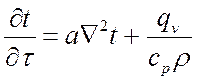Т. к. температурное поле (3) зависит от w_x, w_y, w_z, то необходимо добавить уравнение, описывающее изменение скорости во времени и пространстве. Это позволяет сделать уравнение движения.

5.2.2. Уравнение движения

Уравнение движения дано в курсе гидрогазодинамики. Его упрощенный вывод для одномерного течения состоит в следующем.

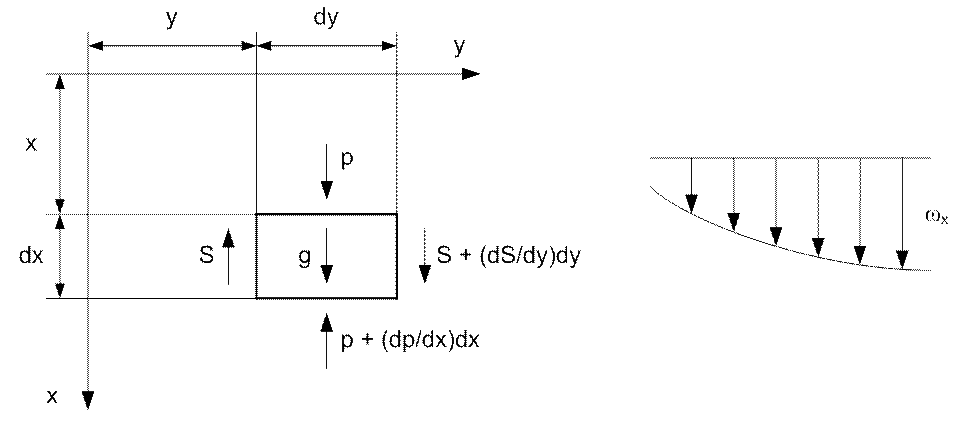
Рис. 40. К выводу уравнения движения

Выделим в потоке вязкой жидкости элемент с размерами dx, dy, dz. Допустим изменение скорости только в направлении оси y произвольным образом.

Силы, действующие на элемент, можно разделить на массовые (объемные) и поверхностные. Массовые силы характеризуются вектором , м²/с, значение которого равно отношению силы, действующей на рассматриваемую частицу, к массе этой частицы. Если на частицу действует сила тяжести, то , где  – ускорение свободного падения.

Поверхностные силы оцениваются отношением силы, действующей на элемент, к величине площади этого элемента (например, силы трения, силы давления).

Таким образом, на элемент действуют три силы: сила тяжести, равнодействующая сил давления и равнодействующая сил трения.

Определим проекции этих сил на ось Ox:

1) Сила тяжести df₁ приложена в центре элемента, она равна произведению проекции g_x на массу элемента :

                                                           .