Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 4

Стационарное поле – это когда температура в различных точках тела постоянна во времени: , .

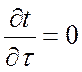Нестационарное поле – это когда температура в различных точках тела не постоянна, а изменяется во времени.

В зависимости температуры от числа пространственных координат температурное поле может быть одномерным: , двухмерным: , трехмерным: .

Одномерное , .

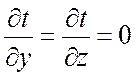Двухмерное , .

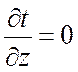Трехмерное .

Для одномерного стационарного поля , .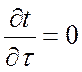

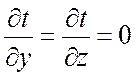2.2. Температурный градиент

Если соединить точки тела, имеющие одинаковую температуру, получим поверхность равных температур, называемую изотермической. Отсюда определение.

Изотермической поверхностью называется совокупность точек, имеющих равную температуру.

Поскольку одна и та же точка не может иметь в одно и то же время различные температуры, то изотермические поверхности не пересекаются. Они либо оканчиваются на граничных поверхностях тела, либо располагаются внутри самого тела.

Сечение изотермических поверхностей плоскостью дает на этой плоскости семейство изотерм. Они обладают теми же свойствами, что и изотермические поверхности: не пересекаются, не обрываются внутри тела, оканчиваются на границах тела либо располагаются внутри самого тела.

Изменение температуры в теле происходит в направлении пересечения изотермических поверхностей. При этом наибольший перепад температуры на единицу длины происходит в направлении нормали к изотермической поверхности.

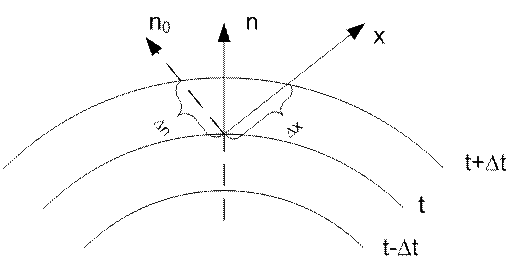
Рис. 1. Изотермы

Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной от температуры по этому направлению, т. е.

                                                    ,

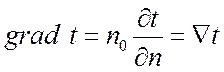где   n₀ – единичный вектор, нормальный к изотермической поверхности и направленный в сторону возрастания температур; n₀ определяет направление температурного градиента.

         – скалярная величина температурного градиента.

По физическому смыслу температурный градиент выражает изменение температуры в градусах (K), приходящееся на 1 м расстояния между изотермическими поверхностями по нормали. Чем больше значение температурного градиента, тем неравномернее распределение температуры в данном теле. Если все точки тела имеют одинаковую температуру, то . Величина  в направлении убывания температуры отрицательна и называется падением температуры.

Проекции вектора  на координатные оси Ox, Oy, Oz равны:

                                             ,

                                            ,

                                             .

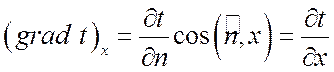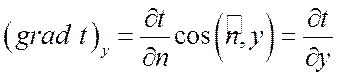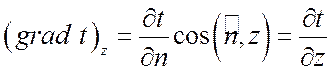Размерность  K/м или °C/м.

2.3. Тепловой поток. Закон Фурье

Количество тепла Q, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком.

Тепловой поток, приходящийся на 1 м² поверхности, называется удельным тепловым потоком или плотностью теплового потока q (иногда его называют тепловой нагрузкой поверхности).

Согласно гипотезе Фурье, количество тепла dQ_t, проходящее через элемент изотермической поверхности dF за промежуток времени dt, пропорционально температурному градиенту Ñt:

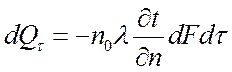                                                , Дж.

Коэффициент пропорциональности l называется коэффициентом теплопроводности, являющийся физическим параметром вещества и указывающим способность вещества проводить тепло.

                                                           l, Вт/(м·K).

Плотность теплового потока есть вектор, определяемый выражением:

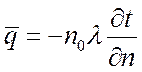                                                     , Вт/м².

Вектор плотности теплового потока  направлен по нормали к изотермической поверхности в сторону убывания температуры, т. к. тепло передается от более нагретых частей тела к более холодным, т. е. противоположно вектору .

Линии, касательные к , являются векторами удельного теплового потока и называются линиями теплового потока.

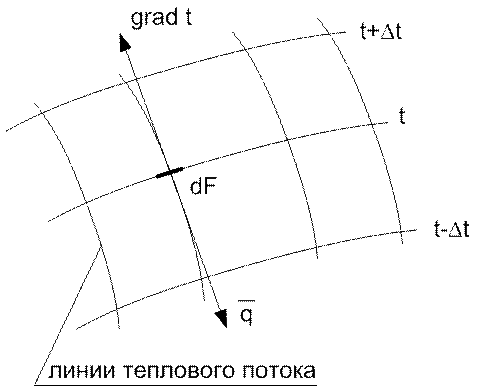
Рис. 2. Связь векторов теплового потока и градиента температуры

Скалярная величина вектора плотности теплового потока равна

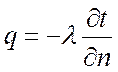                                                      , Вт/м².