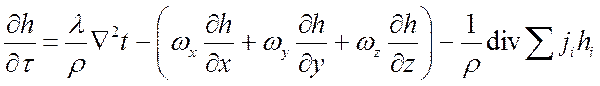 . (*)
. (*)
Здесь ![]() – локальное изменение
энтальпии, вызванное процессами теплопроводности, конвекции и молекулярной
диффузии.
– локальное изменение
энтальпии, вызванное процессами теплопроводности, конвекции и молекулярной
диффузии.
Это уравнение кратко можно записать:
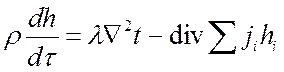 , (**)
, (**)
где 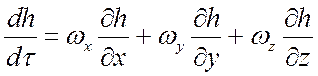 .
.
Таким образом, удельная энтальпия смеси определяется удельными энтальпиями hi и относительными концентрациями компонентов mi по правилу аддитивности:
![]() .
.
Полагая, что ![]() и
и ![]() , где cp
– изобарная теплоемкость смеси, имеем после дифференцирования:
, где cp
– изобарная теплоемкость смеси, имеем после дифференцирования:

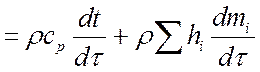 .
.
Используя уравнение массообмена:
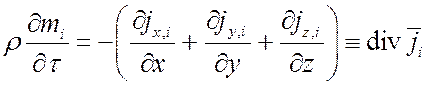 ,
,
получим:
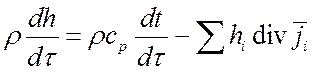 .
.
Подставим полученное выражение в (**):
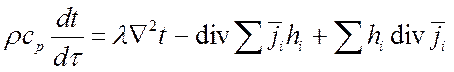 . (***)
. (***)
Согласно правилу дифференцирования произведения двух переменных второй член уравнения преобразуем:
![]() .
.
Но:
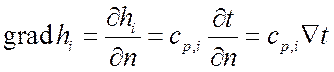 .
.
Подставляем это выражение в (***):
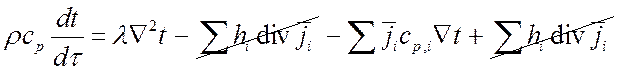 .
.
Подставляем значение ji по закону Фика с учетом того, что термодиффузия и бародиффузия отсутствуют, и перенос массы определяется лишь концентрационной диффузией:
![]() ,
,
где 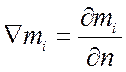 .
.
Но поскольку для бинарной смеси ![]() и
и
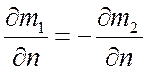 , то
, то ![]() .
Тогда:
.
Тогда:
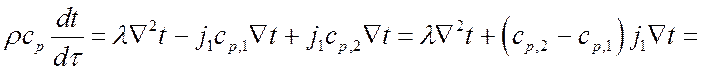
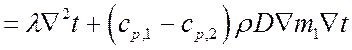 .
.
Таким образом, уравнение энергии бинарной смеси будет:
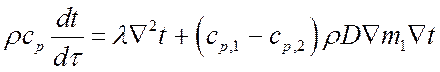 .
.
Это дифференциальное уравнение второго порядка.
Следствие: при ![]() , т. е.
, т. е. ![]() результирующий диффузионный перенос
теплоты (энтальпии) отсутствует, и уравнение энергии переходит в уравнение
энергии конвективного теплообмена:
результирующий диффузионный перенос
теплоты (энтальпии) отсутствует, и уравнение энергии переходит в уравнение
энергии конвективного теплообмена:
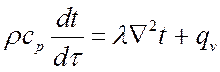 ,
,
или
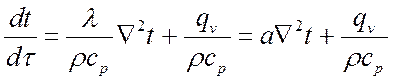 .
.
При отсутствии внутренних источников тепла ![]() :
:
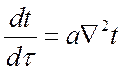 ,
,
где 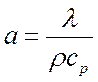 – коэффициент
температуропроводности.
– коэффициент
температуропроводности.
Следует иметь в виду, что:
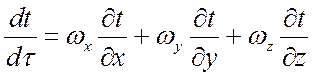 .
.
Анализ уравнения энергии показывает, что температурное поле движущейся среды зависит от составляющих скорости wx, wy, wz и относительного массосодержания. Поэтому к уравнению энергии необходимо добавить уравнение массообмена (сохранения массы) и уравнение движения, записанное для всей смеси в целом. Кроме того, нужно добавить уравнение сплошности для смеси.
Для формирования краевой задачи и решения уравнений для смесей газов необходимо присоединить условия однозначности. В условиях массообмена задание граничных условий имеет некоторые особенности. Для их выяснения рассмотрим процессы теплоотдачи и массоотдачи в бинарную среду и от нее.
В движущейся газовой и жидкой однокомпонентной среде теплота передается теплопроводностью и конвекцией. Процесс передачи тепла называется конвективным теплообменом.
По аналогии, перенос вещества в многокомпонентной среде, происходящий одновременно с процессами молекулярной диффузии и конвекции, называют конвективным массообменном.
Практический интерес представляют процессы теплообмена и массообмена при испарении, сублимации (возгонке), конденсации, сорбции, десорбции и др. В этих случаях система считается гетерогенной. Поверхность жидкости или твердой фазы играет роль приемника тепла в процессе теплоотдачи. Одновременно между этой поверхностью и окружающей средой протекает и процесс массоотдачи.
Для процесса теплоотдачи в расчетах используется закон Ньютона-Рихмана:
![]() ,
,
где qc – тепло, переданное от стенки или на стенку, Дж/(м2·K);
tc – температура стенки, °C;
t0 – температура окружающей среды, °C.
Для процесса массоотдачи используют уравнение:
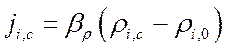 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.