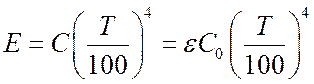 ,
Вт/м2.
,
Вт/м2.
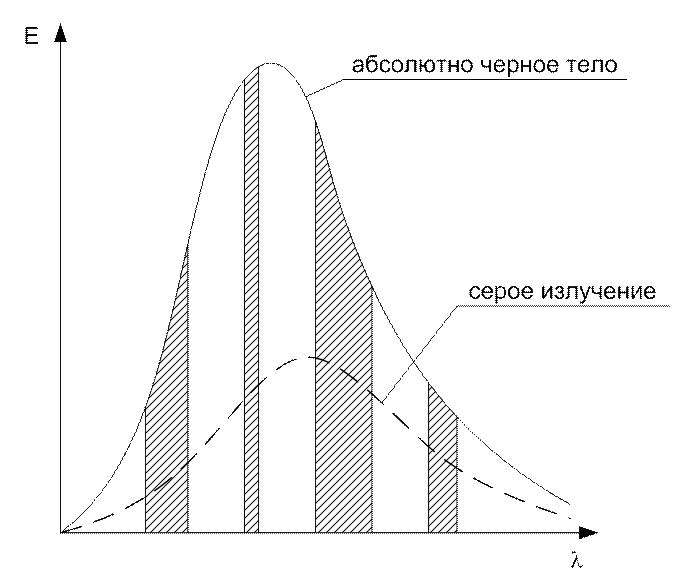
Рис. 45. Серое излучение
Устанавливает связь между плотностью интегрального полусферического излучения и поглощательной способностью тел.
Допустим, имеем два тела: реальное с температурой T и абсолютно черное с температурой T0.
Пусть ![]() . С тела на абсолютно черное тело падает
энергия E, которая им полностью поглощается.
Абсолютно черное тело излучает энергию E0,
часть которой телом в количестве
. С тела на абсолютно черное тело падает
энергия E, которая им полностью поглощается.
Абсолютно черное тело излучает энергию E0,
часть которой телом в количестве ![]() поглощается, а часть
поглощается, а часть ![]() отражается, и, попадая на абсолютно
черное тело, полностью поглощается.
отражается, и, попадая на абсолютно
черное тело, полностью поглощается.
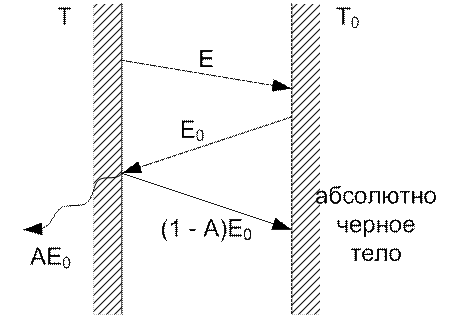
Рис. 46. К выводу закона Кирхгофа
Энергетический баланс лучистого обмена:
![]() .
.
При ![]() , когда наступит
термодинамическое равновесие, тепловое излучение между поверхностями
происходит, но
, когда наступит
термодинамическое равновесие, тепловое излучение между поверхностями
происходит, но ![]() . Формальная формулировка этого
явления такова: при термодинамическом равновесии отношение излучательной
способности к поглощательной для всех тел одинаково и равно излучательной
способности абсолютно черного тела при той же температуре. Тогда:
. Формальная формулировка этого
явления такова: при термодинамическом равновесии отношение излучательной
способности к поглощательной для всех тел одинаково и равно излучательной
способности абсолютно черного тела при той же температуре. Тогда:
![]() , т. е.
, т. е. 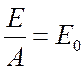 .
.
Это соотношение можно распространить на любые тела, поэтому:
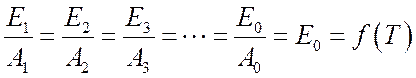 , т.
к.
, т.
к. ![]() .
.
Подставляя формулировку Стефана-Больцмана, получим:
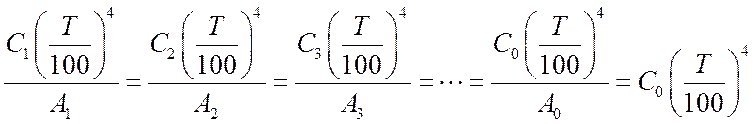 ,
,
или
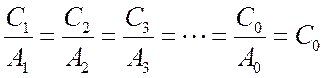 , т.
к.
, т.
к. ![]() .
.
Из этого равенства имеем:
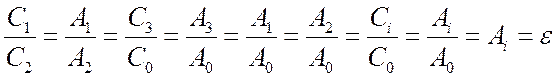 , т. к.
, т. к. ![]() .
.
![]() .
.
При термодинамическом равновесии поглощательная способность и степень черноты тела численно равны между собой.
Устанавливает связь между количеством излучаемой телом энергии и направлением излучения.
Количество энергии, излучаемое элементом поверхности dF1 в направлении элемента поверхности dF2 пропорционально количеству энергии, излучаемому
этим элементом поверхности в направлении нормали dQn,
умноженному на пространственный угол dW и ![]() , где j – угол, образованный направлением
излучения и нормалью к излучаемой поверхности:
, где j – угол, образованный направлением
излучения и нормалью к излучаемой поверхности:
![]() , Вт.
, Вт.
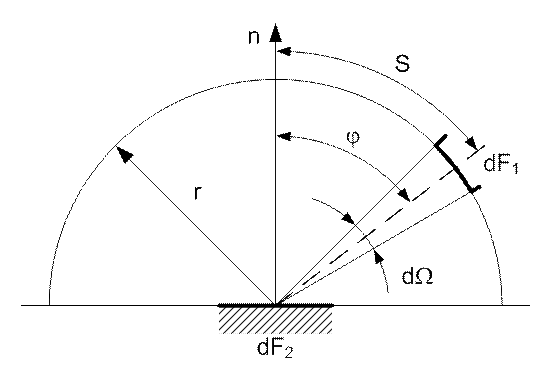
Рис. 47. Зависимость энергии излучения от угла илучения
Следовательно, наибольшее количество энергии излучается
поверхностью dF1 в направлении
нормали при ![]() . С увеличением j количество энергии уменьшается и при
. С увеличением j количество энергии уменьшается и при ![]() °
становится равной нулю.
°
становится равной нулю.
![]() ,
,
где En – плотность излучения площадки dF1 в направлении нормали.
![]() . (*)
. (*)
Плоский угол j
измеряется величиной ![]() , где r – радиус круга, S – длина
дуги, на которую опирается угол j.
Бесконечно малая величина плоского угла
, где r – радиус круга, S – длина
дуги, на которую опирается угол j.
Бесконечно малая величина плоского угла ![]() .
.
По аналогии, телесный угол W, измеряемый в стерадианах (ср), представляет сферу радиуса r с центром в вершине этого угла. Площадь сферы этого угла – f. Тогда:
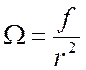 ,
, 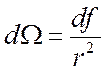 .
.
Обозначим: y
– долгота, j – полярное
расстояние, тогда на сфере вырезается сферический прямоугольник по направлениям
![]() и
и ![]() , бесконечно
малый угол dW и четырехугольник df. Стороны
этого четырехугольника df:
, бесконечно
малый угол dW и четырехугольник df. Стороны
этого четырехугольника df: ![]() и
и ![]() .
Тогда:
.
Тогда:
![]() .
.
Интегрируя выражение (*) по углам j и y, получим:
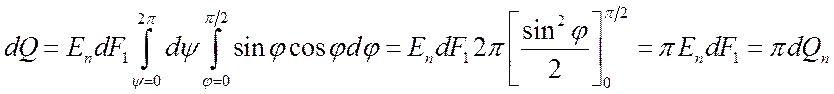 .
.
Энергия излучения элементом поверхности dF1:
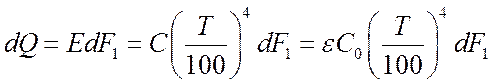 .
.
Приравнивая к предыдущему, получим:
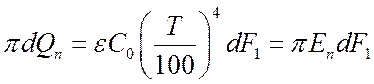 .
.
Тогда:
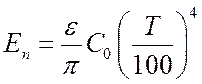 .
.
Плотность излучения в направлении нормали в p раз меньше полной плотности излучения. Тогда:
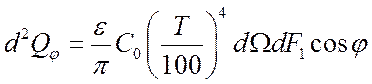 .
.
Количество энергии, приходящейся на единицу облучаемой поверхности называется облучаемой способностью источника излучения. Кеплером установлено, что точечный источник излучает равномерно во все стороны энергию в количестве W, Вт, а для сферы радиусом r:
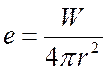 .
.
Количество энергии, приходящейся на облучаемую площадку dF, будет:
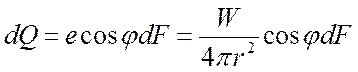 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.