Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 49

Суммарный же удельный поток массы за счет молекулярного и конвективного переноса:

                                                          .

Вместе с массой вещества переносится энтальпия , где h_i – энтальпия i-го компонента, Дж/кг. Через контрольный участок поверхности переносится энтальпия . Следовательно, плотность теплового потока:

                                                     ,

где   , здесь  – удельная энтальпия смеси;

         – градиент температуры.

Тогда:

                                              .

В этом уравнении первый член учитывает перенос теплоты теплопроводностью, второй – конвекцией, третий – молекулярной диффузией.

Для сравнения, в однокомпонентной движущейся жидкости (среде):

                                          , здесь .

9.2. Дифференциальные уравнения тепломассообмена

Для вычисления теплового потока в условиях тепломассопереноса следует определить поля температур, скоростей и потоков массы.

9.2.1. Уравнение массообмена

Предположим, что в элементе жидкость несжимаема, в нем нет источников массы, отсутствуют термо- и бародиффузия.

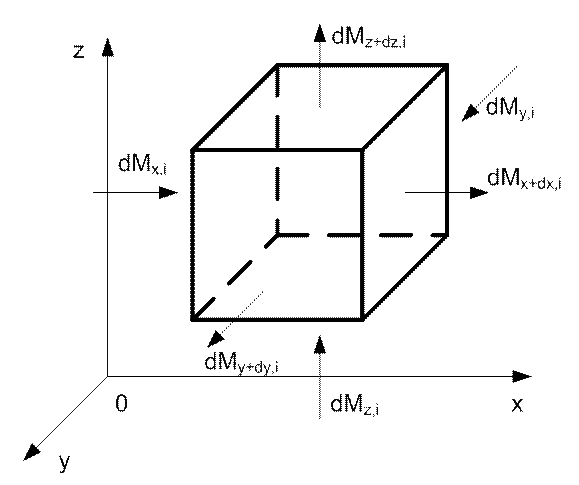
Рис. 87. К выводу уравнения массообмена

Размеры элемента dx, dy, dz. Считаем, что D и r постоянны. Установим баланс массы в элементе.

По оси x за время dt вносится в элемент масса i-го компонента в количестве:

                                                     ,

а выносится за это же время:

                                                  .

Перенос массы по оси x:

                             .

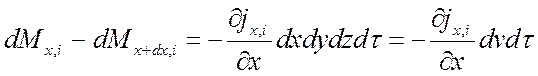Аналогично по другим осям:

                                            ;

                                             .

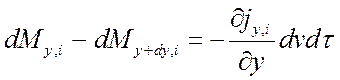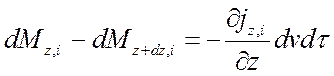Суммируя по трем осям, получим изменение массы i-го компонента:

                                         .

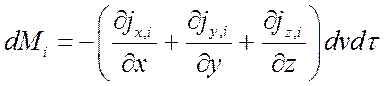Т. к.:

                                                      ,

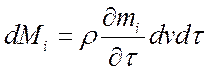то

                                     . (*)

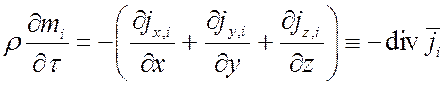Полагая, что масса i-го компонента переносится только концентрационной диффузией и конвекцией, имеем:

                                                 ;

                                                 ;

                                                 .

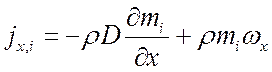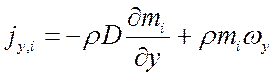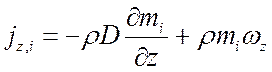Найдем производные:

                                    ;

                                   ;

                                    .

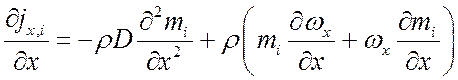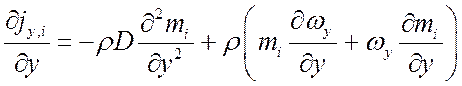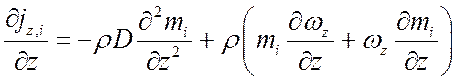Просуммируем и подставим в уравнение (*):

      .

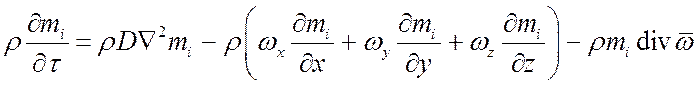При  последний член этого равенства равен нулю, т. е. , т. к. отсутствует перенос за счет ободной конвекции. Тогда:

                                   ,

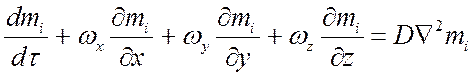или через полный дифференциал:

                                                         .

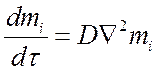Это уравнение сохранения массы i-го компонента среды, движущейся со скоростью .

Для неподвижной среды  уравнение массообмена:

                                                         

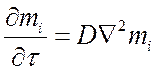
похоже на уравнение теплопроводности .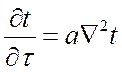

Здесь учтен перенос массы только концентрационной диффузией.

9.2.2. Уравнение энергии

Полагаем, что в бинарной смеси отсутствуют источники теплоты. Пренебрегаем теплотой трения. Принимаем постоянными физические характеристики среды.

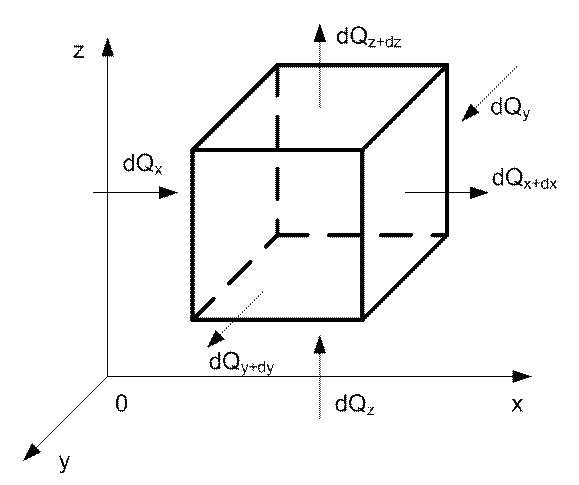
Рис. 88. К выводу уравнения энергии

Выделим элемент с размерами dx, dy, dz. Запишем уравнение теплового баланса. Полагаем, что подведенная теплота идет на изменение энтальпии элементарного объема, а работа расширения равна нулю. Тогда из рассмотренного баланса энергии (см. дифференциальное уравнение энергии теплопроводности, п. 2.5):

                                      .

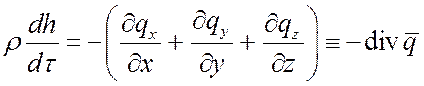Но , следовательно:

                                             ;

                                             ;

                                             .

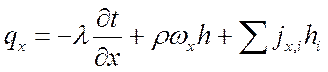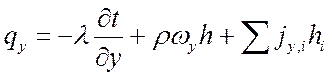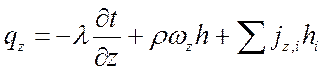Получим:

                             ;

                            ;

                              .

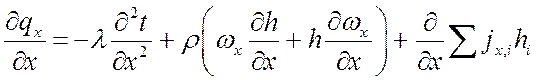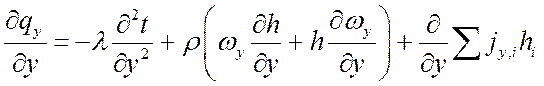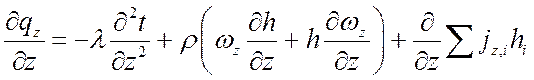Просуммируем и, учтя, что для несжимаемой жидкости , имеем:

.

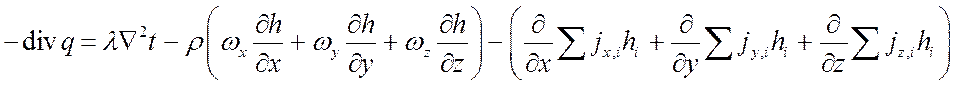Ранее было получено уравнение энергии для теплопроводности в виде:

                                                     .

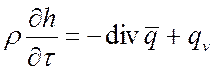Подставляя сюда значение , получим уравнение в виде: