Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 8

в) начальные условия (распределение температуры в теле в начальный момент времени);

г) граничные условия, определяющие взаимодействие тела с окружающей средой.

Геометрическими условиями задаются форма и размеры тела. Физическими условиями задаются физические параметры l, c, r и др., может быть задан закон распределения внутренних источников тепла. Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. Аналитическое выражение может быть записано в виде: при  . При равномерном распределении температуры в теле начальное условие упрощается: при  .

Граничные условия могут быть заданы несколькими способами.

а) Граничные условия первого рода. Задается распределение температуры на поверхности тела как функция координат и времени:

                                                       ,

где   t_c – температура поверхности тела;

        x, y, z – координаты поверхности тела.

В частном случае, если температура поверхности тела постоянна во времени, то

                                                            .

б) Граничные условия второго рода. Задается распределение плотности теплового потока на поверхности тела как функция координат и времени:

                                                       ,

где   q_п – плотность теплового потока на поверхности тела.

В частном случае, при постоянном тепловом потоке по поверхности и во времени условие запишется

                                                        .

Такой случай имеет место при нагревании металлических заготовок в высокотемпературных печах.

в) Граничные условия третьего рода. Задаются температура окружающей среды t_ж и закон теплообмена между поверхностью тела и окружающей средой. Это условие характеризует закон теплообмена между поверхностью и окружающей средой в процессе охлаждения или нагревания тела. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона-Рихмана: количество тепла, отдаваемое (воспринимаемое) единицей поверхности тела, пропорционально разности температур поверхности тела и окружающей среды:

                                                         ,

где   a – коэффициент пропорциональности или коэффициент теплоотдачи, имеет размерность Вт/(м²·K), представляет собой количество тепла, отдаваемое (воспринимаемое) единицей поверхности тела при разности температур между поверхностью тела и окружающей средой в 1 K.

На основании закона сохранения энергии для поверхности тела можно записать и использовать закон Фурье:

                                                   .

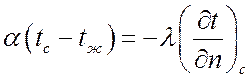Индекс «с» относится к поверхности тела. Таким образом, исходя из равенства тепловых потоков: отводимого от поверхности тела и подводимого к поверхности теплопроводностью из внутренних объемов тела – можно представить граничное условие третьего рода в виде:

                                                   .

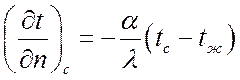г) Граничные условия четвертого рода характеризуют условия теплообмена системы тел, имеющих различные коэффициенты теплопроводности. Предполагается, что между телами осуществляется идеальный контакт (температуры соприкасающихся поверхностей одинаковы). Тогда:

                                                    ,

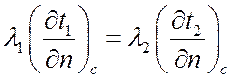где   l₁ и l₂ – коэффициенты теплопроводности первого и второго тела.

В задачах с граничными условиями четвертого рода задается отношение тангенсов углов наклона касательных к температурным кривым в точке соприкосновения тел или тела и среды:

                                                      .

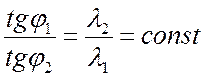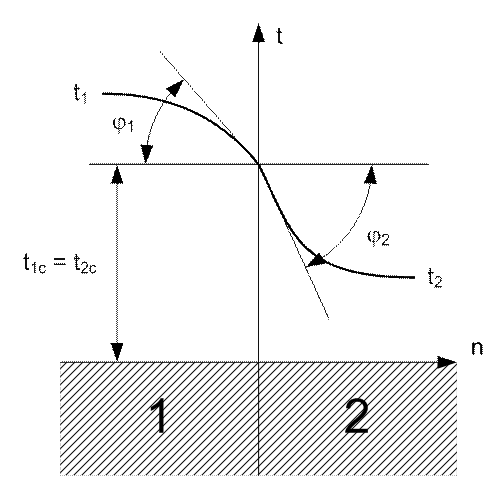
Рис. 6. Граничное условие четвертого рода

Т. к. при совершенном контакте оба тела на поверхности соприкосновения имеют одинаковую температуру, то касательные у поверхности раздела проходят через одну и ту же точку.

Заключение. Полученное дифференциальное уравнение совместно с условиями однозначности дает полную математическую формулировку конкретного закона теплопроводности. Его можно решить аналитическим, численным или экспериментальным методом. В случае применения последнего используются методы физического моделирования или метод тепловых аналогий.