Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 10

Если проинтегрировать выражение 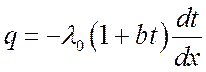 с переменными верхними пределами интегрирования, то получим выражение для температурного поля при :

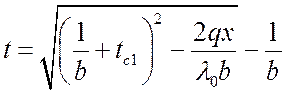                                             , °C,         (*)

где   t – текущее значение температуры в сечении x.

(*) – это уравнение кривой линии. Характер этой температурной кривой определяется знаком и численным значением коэффициента b.

3.1.1.1. Многослойная плоская стенка

При стационарном температурном режиме тепловой поток, проходящий через многослойную плоскую стенку, будет один и тот же, т. е. 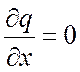. Пусть стенка содержит n слоев, имеющих различные l. Примем также, что контакт слоев совершенен, температуры в месте контакта для соприкасающихся слоев одинаковы.

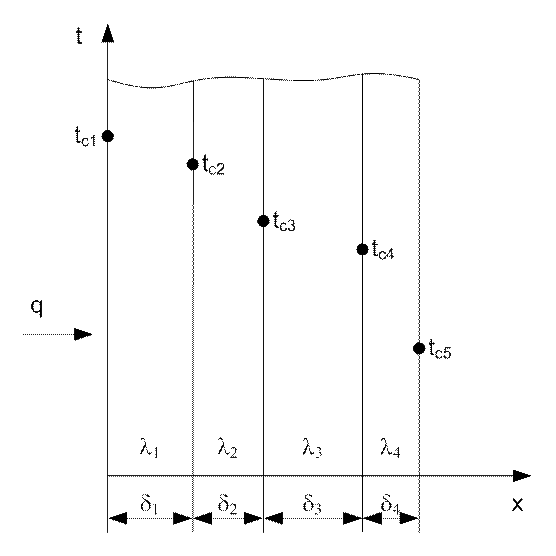
Рис. 9. Теплопроводность через многослойную плоскую стенку

Запишем уравнение для каждого слоя стенки:

                                            , ;

                                           , ;

                                           , ;

                                           , ;

                                                                   …

                                       , ;

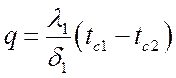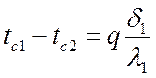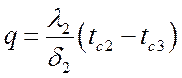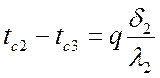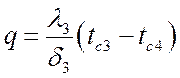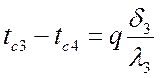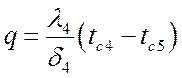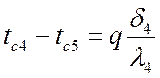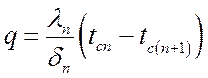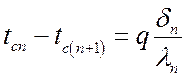Сложив эти уравнения, получим:

                      .

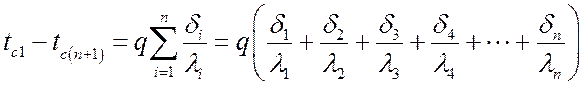Отсюда плотность теплового потока:

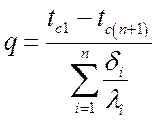                                                   , Вт/м².

Величина 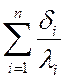 называется термическим сопротивлением теплопроводности многослойной стенки.

Если сравнить процесс переноса тепла через многослойную стенку и стенку из однородного материала, то удобно ввести в рассмотрение эквивалентный коэффициент теплопроводности l_экв многослойной стенки.

Для однослойной стенки .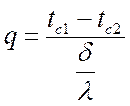

Для многослойной стенки .

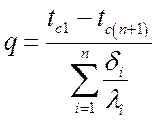Эквивалентный коэффициент теплопроводности равен коэффициенту теплопроводности такой однородной стенки, толщина которой D равна толщине многослойной стенки 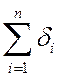, а тепловое сопротивление равно тепловому сопротивлению рассматриваемой многослойной стенки, т. е.

                                                    .

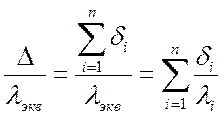Отсюда

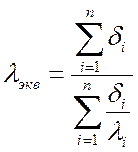                                                  , Вт/(м·K).

Поэтому l_экв зависит не только от теплофизических свойств слоев, но и от толщины этих слоев.

Температуры на границе соприкосновения двух соседних слоев:

                                                         ;

                                                         ;

                                                   .

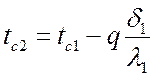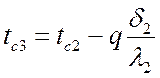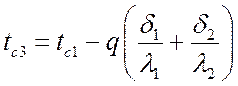В общем виде:

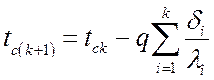                                                  , °C.

Для многослойной стенки температура изменяется по ломаной линии.

3.1.2. Передача тепла при граничных условиях третьего рода (теплопередача)

Передача тепла от одной подвижной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей.

Она включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде.

Рассмотрим теплопередачу через однородную и многослойную плоские стенки.

Пусть имеем однородную стенку толщиной d. Заданы коэффициент теплопроводности стенки l, температуры окружающей среды t_ж1 и t_ж2, коэффициенты теплоотдачи a₁ и a₂.

Рис. 10. Теплопередача через однородную плоскую стенку

По закону Ньютона-Рихмана удельный тепловой поток от горячей жидкости к стенке определяется уравнением:

                                                        .

По закону Фурье тепловой поток через стенку путем теплопроводности:

                                                        .

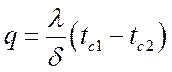Тепловой поток от поверхности стенки к холодной жидкости за счет теплоотдачи:

                                                       .

Вычислим падение температур:

                                                         ,

                                                          ,

                                                        .

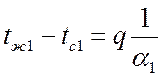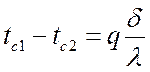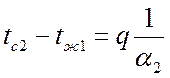После сложения получим:

                                               .

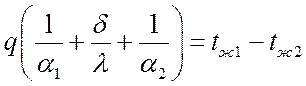Отсюда:

                                                       .

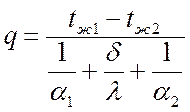Обозначим:

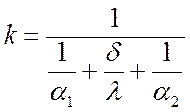                                              , Вт/(м²·K).