Теория теплообмена. Теплопроводность. Основные положения теории теплопроводности. Теплопроводность при стационарном режиме. Теплопроводность при нестационарном режиме. Теплообмен при фазовых превращениях, страница 16

Заданы коэффициенты теплообмена на поверхности стержня. Коэффициент теплопроводности l имеет достаточно большое значение. f – площадь поперечного сечения, u – периметр сечения. При этих условиях считаем, что температура изменяется только вдоль длины стержня, и пренебрегаем ее изменением в поперечном направлении. Стержень находится в среде, температура которой постоянна и равна t_ж, и от которой будем вести отсчет температуры. Тогда избыточная температура будет:

                                                   , .

Выделим на стержне на расстоянии x элемент длиной dx. Тогда можно записать уравнение теплового баланса:

                                                        ,

где   Q_x – количество тепла на входе в элемент в единицу времени;

        Q_x+dx – количество тепла на выходе в элемент в единицу времени;

        dQ – количество тепла, отдаваемое поверхностью стержня в единицу времени.

По закону Фурье:

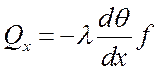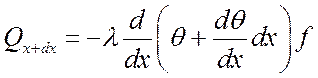                                                      , Вт,

                                          , Вт,

или

                                             .

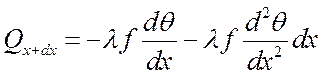Вычитая из первого уравнения второе, получим:

                                                       .

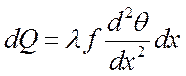С другой стороны, количество тепла, отданное ребром охлаждающей жидкости по закону Ньютона-Рихмана за счет теплоотдачи:

                                                          ,

где   u – периметр стержня, м;

        a – коэффициент теплоотдачи от поверхности стержня, Вт/(м²·K).

Сравнивая полученные выражения, получим:

                                                    ,

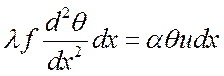или

                                                     ,

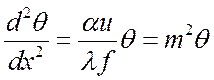или

                                                         ,

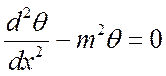где 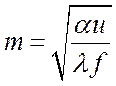  , 1/м.

При  и  величина . Тогда:

                                                      ,

где   C₁ и C₂ – постоянные интегрирования, определяемые из задаваемых граничных условий, зависящих от длины, формы стержня и других факторов.

3.6.2. Теплопроводность стержней

3.6.2.1. Стержень бесконечной длины

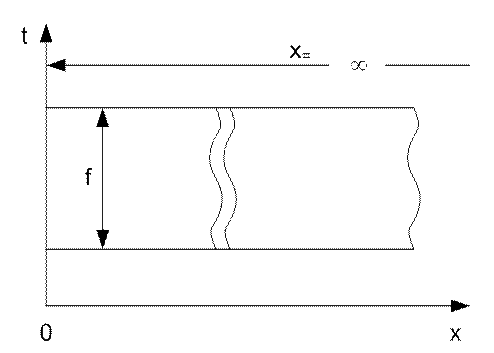
Рис. 21. Теплопроводность в стержне бесконечной длины

В начальном сечении стержня температура поддерживается постоянной, т. е. при  . Если , то все тепло будет отдано стержнем в окружающую среду, и при  . Наложив такие граничные условия, получим:

                                    при  , т. к. ;

                                     при  , т. к. : .

Последнее равенство  возможно при . Тогда , и в конечном виде:

                                                         , °C.                      (*)

Безразмерная температура 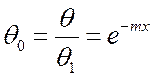 выражена в долях от начальной температуры стержня q₁ в зависимости от длины стержня.

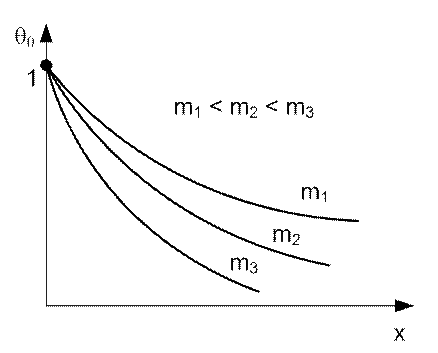
Рис. 22. Изменение безразмерной температуры q₀ по длине стержня при различных значениях параметра m

Из графика видно, что безразмерная температура убывает тем сильнее, чем больше параметр m. При  .

Из уравнения 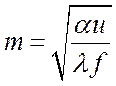  характеризует теплоотдачу с поверхности стержня, а  – теплопроводность вдоль стержня. Выбор материала стержня с большим l приводит к уменьшению m и менее резкому падению температуры вдоль стержня. При 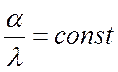 m возрастает с ростом , что указывает на более эффективную работу ребер с профилями, имеющими большее отношение  при том же поперечном сечении, когда речь идет об охлаждении изделий.

Количество тепла, передаваемое стержнем в окружающую среду, равно теплу, проходящему через его основание:

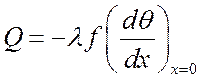                                                   , Вт.

Дифференцируя выражение (*), получим:

                                            .

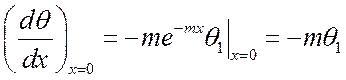Тогда при  количество тепла, переданное в окружающую среду:

                                              , Вт.

3.6.2.2. Стержень конечной длины

В отличие от п. 3.5.2.1, граничные условия будут другими:

а)     при  ;

        при  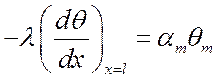 – балансовое уравнение, или ,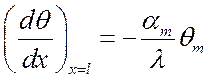

где   a_т и q_т – коэффициент теплоотдачи с торца стержня и температура на конце стержня.

При  имеет место равенство количества тепла, подведенного к торцу стержня за счет теплопроводности стержня, количеству тепла, теряемого стержнем через торец в окружающую среду через теплоотдачу.