Математическая статистика в горно-геологических расчетах, страница 45

·  ANOVA/MANOVA –  Модуль дисперсионного анализа

·  Classification Trees – Модуль Классификационное дерево

·  Data Management – Модуль Управление данными

·  Quality Control –Модуль Контроль качества

Более подробная информация  о работе с данными в среде  STATISTICA содержится в [3 ]

        Для примера возьмем задачу о нахождении уравнения множественной регрессии, которая решалась нами средствами пакета Mathcad   в пункте 5.8 и в среде Excel в пункте 6.1.

а) Заполняем данными исходную таблицу ( приводим фрагмент таблицы):

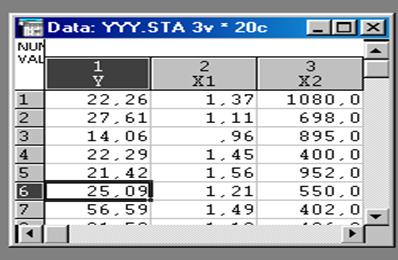
б) Используя переключатель модулей, переходим в модуль  Множественная регрессия.

Выбираем зависимые (dependent -У)  и независимые (independent X₁, X₂)    переменные (variables). После нажатия кнопки ОК результаты можно вывести в виде таблицы

 Здесь R=0,782 – корреляционное отношение; RI=0,612 – коэффициент детерминации; F(2,17)=13,389 – наблюдаемое значение критерия Фишера; p<0,00032 – значимость ошибки первого рода, при которой гипотезу об адекватности полученной модели нужно отвергнуть. Малая вероятность говорит о том, что модель адекватная.

Параметры модели содержатся в столбце В. Они совпадают с найденными ранее. В следующих столбцах помещены СКО этих параметров; их  t-статистики и уровни вероятностей ошибок. Если выбрать значимость a=0,1 ,  то коэффициенты регрессии при Х₁  и Х₂ признаются значимыми, свободный член уравнения регрессии признается незначимым. Это значит, что нужно выбрать другую спецификацию модели, возможно без свободного члена.