Пусть выборка задана дискретным статистическим рядом:
|
х i |
х 1 |
х 2 |
… |
х i |
… |
х k |
|
ni |
n 1 |
n 2 |
… |
n i |
… |
n k |
В этом случае расчетные формулы имеют вид:
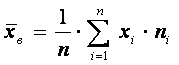 ,
,
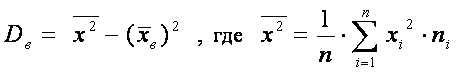 ,
,
![]() ,
,
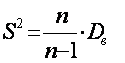 ,
, ![]() ,
,
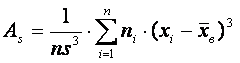 ,
, 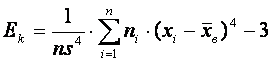 .
.
Мода Мо по дискретному ряду равна тому значению хm, которому соответствует наибольшая частота nm .
Медиана Ме рассчитывается по вариационному (отсортированному) ряду так: если объем выборки – нечетное число n=2m+1, то медиана равна варианте с номером m+1 в этом отсортированном ряду Ме=хm+1 ; если же объем выборки – четное число n=2m, то медиана равна среднему арифметическому из двух центральных вариант Ме=0,5×(хm + хm+1).
Если выборка задана интервальным статистическим рядом:
|
Интервал |
х 1 – х 2 |
х 2 – х 3 |
… |
х i–1 – х i |
… |
х k –1 – х k |
|
ni |
n 1 |
n 2 |
… |
n i |
… |
n k |
то в этом случае заменяют интервалы их серединами и используют формулы для дискретного ряда.
В отличие от дискретных рядов определение моды и медианы требует проведение специальных расчетов.
Мода вычисляется по формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.