Математическая статистика в горно-геологических расчетах, страница 38

Запишем решение системы по правилу Крамера:

a = D1/D=5,541; b = D2/D=–1,128; c = D3/D=6,48.

Следовательно, уравнение нелинейной параболической регрессии имеет вид :

            = 5,541 –6,128х +6,48х²   .

Пункт 11. Построим полученные линии регрессии в одной системе координат.

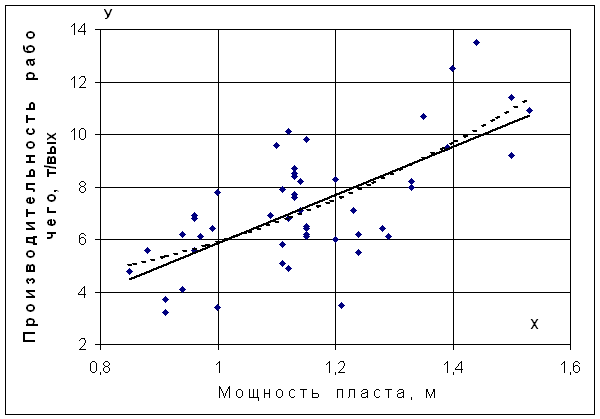
Здесь сплошная линия представляет линейную регрессию, а пунктирная линия  – параболическую регрессию.

Пункт 12. Для всех моделей рассчитаем теоретический коэффициент детерминации и теоретическое корреляционное отношение; среднюю квадратическую погрешность уравнения; среднюю относительную погрешность аппроксимации.

Используем уравнение линейной регрессии   = 9,21×х – 3,36

и параболической регрессии   = 5,541 –6,128х +6,48х², вычислим теоретические значения признака У. Заполним таблицы.

Для краткости записей расчетные таблицы приводим не полностью.

а) Для линейной регрессии   = 9,21×х – 3,36