по С2: n2 – количество испытаний; m2 – частота появления события А в этих испытаниях, w2 = m2/ n2 – относительная частота (выборочная доля) события А в совокупности С2.
Требуется при заданном уровне значимости a установить равенство вероятностей р1 и р2 .
Выдвинем основную и альтернативную гипотезы. Рассмотрим три случая:
а) Н0: р1 = р2 б) Н0: р1 = р2 в) Н0: р1 = р2
Н1: р1 > р2 Н1: р1 < р2 Н1: р1 ¹ р2
Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия
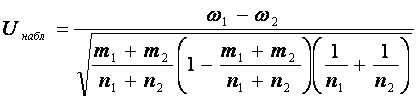
Критические области и точки зависят от выдвинутых альтернативных гипотез H1 .
а) Н1: р1 > р2
Критическая область является правосторонней. Критическая точка uкр находится из равенства Ф(uкр)= (1–2a)/2 , где функция Лапласа Ф(х) задается таблицей (приложение 2); a – заданный уровень значимости.
Если в результате сравнения окажется Uнабл < uкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Uнабл > uкр, то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
б) Н1: р1 < р2
Критическая область является левосторонней. Сначала находят вспомогательную точку uкр' из равенства Ф(uкр')= (1–2a)/2, тогда критическая точка равна uкр = – uкр' .
Если в результате сравнения окажется Uнабл > uкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Uнабл < uкр, то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
в) Н1: р1 ¹ р2
Критическая область является двусторонней. Критическая точка uкр находится из равенства Ф(uкр)= (1–a)/2 , где функция Лапласа Ф(х) задается таблицей (приложение 2).
Если в результате сравнения окажется ½Uнабл½ < uкр, то нет оснований отвергнуть нулевую гипотезу H0; если же ½Uнабл½ > uкр, то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
Пусть эмпирическое распределение задано интервальным статистическим рядом
|
Интервал |
х 1 – х 2 |
х 2 – х 3 |
… |
х i–1 – х i |
… |
х m –1 – х m |
|
ni |
n 1 |
n 2 |
… |
n i |
… |
n m |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.