Математическая статистика в горно-геологических расчетах, страница 23

Исправленная СКО   S²_x1 =14,44×7/6 = 16,84

Параметры признака Х₂ рассчитываются аналогично:

n=8;     10;     116,625 ;

D_в = 116,625 – 10² = 16,625 :    S²_x2 =16,625×8/7 = 19  .

Вопрос эффективности применения новой технологии сводится к проверке статистической гипотезе о равенстве двух средних (математических ожиданий) генеральных совокупностей. Для корректного решения необходимо убедиться в равенстве дисперсий указанных генеральных совокупностей (п. 2.4.1).

Выдвинем основную и альтернативную гипотезы. 

     Н₀: D(Х₂) = D(Х₁)                                          

     Н₁: D(Х₂) > D(Х₁)                                 

Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия (отношение большей дисперсии к меньшей):

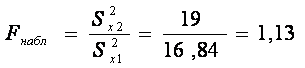
Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Фишера–Снедекора (приложение 7)

при a =0,01;    k₁ = 8 –1 = 7;  k₂ = 7 –1 = 6

F_кр=F(0,01;7;6) = 8,26

В результате сравнения получим F_набл < F_кр. Значит,  нет оснований отвергнуть нулевую гипотезу H₀. Следовательно, принимаем гипотезу о равенстве дисперсий двух генеральных совокупностей.

          Для выяснения эффективности применения новой технологии   проверим статистическую гипотезу о равенстве двух средних генеральных совокупностей (п. 2.4.2).

Выдвинем основную и альтернативную гипотезы.

     Н₀: M(Х₁) = M(Х₂)      

     Н₁: M(Х₁) > M(Х₁)           

Принятие нулевой гипотезы Н₀  даст основания считать, что новая система технологии добычи угля не приводит к изменению засорения угля.

Принятие гипотезы H₁ будет значить, что новая система технологии  приводит к уменьшению засорения угля, и, следовательно, она эффективна.

Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия                 

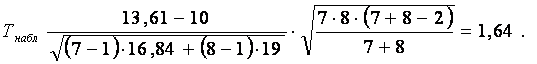
Этот критерий является случайной величиной, которая подчиняется закону распределения Стьюдента с  k =7+8–2=13  степенями свободы.

Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, односторонняя критическая область)  

 t_кр = t(0,01;13) = 2,65.

В результате сравнения получим T_набл < t_кр . Значит,  нет оснований отвергнуть нулевую гипотезу H₀. Следовательно, новая система технологии не приводит к изменению качества угля по засорению. Она не эффективна.

Пример 2

При уровне значимости a=0,05  проверить гипотезу о нормальном законе распределения генеральной совокупности  признака У  из задачи 1 (п. 2.3) , используя критерий Пирсона.

Проверим гипотезу о нормальном распределении признака Y. Используем критерий Пирсона.

Нормальный закон распределения является двухпараметрическим распределением с параметрами а и s. Значит,  r = 2. Из выборки по У возьмем оценки параметров распределения:

  а »  =7,284;   s » S _у = 2,254 .

Для каждого интервала признака У необходимо вычислить вероятности попадания признака  в данный интервал. Используем готовую формулу из теории вероятности для величины, распределенной нормально: