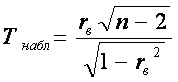Математическая статистика в горно-геологических расчетах, страница 30

                          .

Этот критерий является случайной величиной, которая подчиняется закону распределения Стьюдента с  k = n – 2 степенями свободы. Критическая область является двусторонней. По таблице критических точек распределения Стьюдента (Приложение 6)  определяется критическое значение критерия при выбранном уровне значимости ошибки a  и числе степеней свободы k :

 t_кр = t_кр (α; k).

Если  Т_набл > t_кр , то нулевая гипотеза отвергается. Это значит, что коэффициент корреляции значимо отличается от нуля  и признаки  Х  и  У коррелированы.

Если  Т_набл < t_кр , то нулевая гипотеза  не отвергается. Это значит, что коэффициент корреляции незначимо отличается от нуля  и признаки  Х  и  У некоррелированы.

5.6 Теоретический коэффициент детерминации и теоретическое корреляционное отношение

          Теоретический коэффициент детерминации и теоретическое корреляционное отношение определяются по уравнению регрессии :

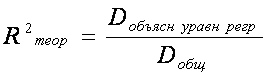 , где D_{обїясн уравн регр} – дисперсия результативного признака У, объясненная уравнением регрессии; D_общ – общая дисперсия результативного признака У .

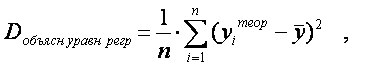                      (8)

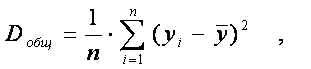
n – объем выборки;

y_i – индивидуальные значения результативного признака У;

 – среднее значение признака У;

y_i^теор – индивидуальные значения результативного признака У, рассчитанные  по уравнению регрессии: y_i^теор=f(x_i); если уравнение регрессии линейное, то y_i^теор=kx_i + b, а корреляционное отношение совпадает с  модулем коэффициента корреляции η = êr_в ê, коэффициент детерминации равен  R²= r_в² .

Коэффициент детерминации характеризует тесноту связи между признаками. В количественной форме он указывает какая часть общей дисперсии результативного признака  У объясняется вариаций признака Х. Например, если построена статистическая модель, описывающая зависимость объема суточной добычи (У) от мощности пласта (Х) и коэффициент детерминации равен 0,56, то это значит, что 56% дисперсии  объема суточной добычи объясняется по выбранной модели вариацией мощности пласта.

Для получения выводов о практической значимости синтезированной модели используются качественные оценки, которые даются на основе шкалы Чеддока [8].

5.7 Нелинейная корреляция 

          Если график регрессии – кривая линия, то корреляцию называют криволинейной. Параметры уравнения криволинейной регрессии  находят по методу наименьших квадратов, а в некоторых случаях сводят задачу к линейной регрессии путем введения соответствующих замен. Ниже приводятся наиболее типичные случаи криволинейной регрессии.