Математическая статистика в горно-геологических расчетах, страница 31

а) Параболическая зависимость 

Параметры регрессии a, b, c  находятся из решения системы:

                                       (9)

б) Гиперболическая зависимость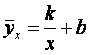 

Делаем замену   и сводим задачу к линейной регрессии .  Параметры  k  и b находятся по формулам линейной регрессии ( с точностью до обозначений):

   ,

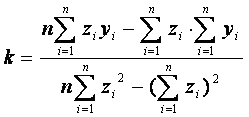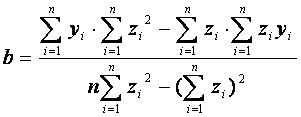   .                                (10) 

где      .

в) Логарифмическая зависимость 

Делаем замену   и сводим задачу к линейной регрессии .

г) Экспоненциальная зависимость 

Делаем замену    z = e^x  и сводим задачу к линейной регрессии .

д) Степенная  зависимость 

Делаем замену   z = x^m   и сводим задачу к линейной регрессии .

Теснота связи между результативным признаком Х и фактором У при нелинейной форме их связи оценивается при помощи коэффициента детерминации R², который находится по той же формуле (8) из  п.5.6, что и для линейной связи. Качественная оценка тесноты связи производится по шкале Чеддока.

          Аналогом коэффициента корреляции для нелинейного случая служит корреляционное отношение   .

5.8 Множественная регрессия

          Поскольку в горном деле важные производственные показатели  чаще всего объясняются несколькими факторами, то для  их прогноза применяется множественная регрессия, параметры которой определяются также по методу наименьших квадратов.

Общий вид модели:   , 

где  х₁, х₂, …, х_k   – независимые факторы, а  у – результирующий показатель. При этом функция множественной регрессии   может быть как линейная, так и нелинейная.

Очень важным является вопрос о том, сколько независимых факторов может быть в уравнении множественной регрессии при заданном объеме выборки n. Обычно используют такое правило: число наблюдений должно быть  не менее чем в 8-10 раз  больше числа факторов в уравнении регрессии.

          Наиболее удобная форма расчета линейной множественной регрессии – матричная. Приведем расчетные формулы, которые можно легко реализовать   в компьютере при помощи пакета программ Mathcad.

Пусть искомое уравнение регрессии имеет вид:  .

Введем  матрицу оценок параметров регрессии 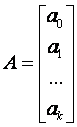 . Она неизвестна.

Для составления регрессии возьмем выборку объема n  и  запишем наблюдаемые значения  признаков  Х₁, Х₂, …, Х_k   и  У. 

На основании  полученных данных запишем матрицы:

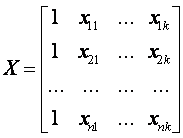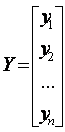 ,        . Здесь  х_ij  обозначает наблюдаемое значение i - го  признака для  j-го наблюдения.