Математическая статистика в горно-геологических расчетах, страница 28

Из последнего столбца таблицы находят наибольшее из полученных модулей

  n ×D = max{n×ôF_n(x) – ×F(x)ô} = 2,16.

Определяем наблюдаемое значение критерия согласия Колмогорова

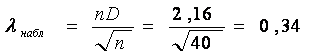                       .                             Этот критерий является случайной величиной, которая подчиняется закону распределения  Колмогорова.

По таблице критических точек (приложение 8), используя заданный уровень значимости a = 0,2  находят критическое значение критерия

         l_кр =  l(0,2) = 1,07.

Сравниваем: l_набл < l_кр, значит, нет оснований отвергнуть нулевую гипотезу H₀. Следовательно, гипотезу о  показательном законе  распределения времени безотказной работы стопора можно считать правдоподобной.

5 Элементы корреляционного и регрессионного анализа

          Зависимость между переменными случайными величинами Х и У, при которой каждому значению одной из них соответствует определенное среднее значение другой величины, называется корреляционной.  Функция, описывающая такую зависимость, называется регрессией. По виду функции  различают  линейную и нелинейную регрессии, по количеству зависимых переменных –  одномерную и множественную регрессии. Признак Х, соответствующий независимой переменной, будем называть факторным, признак У, соответствующий зависимой переменной, будем называть результативным.

5.1 Корреляционное поле

Пусть статистические данные представляют собой ряд пар связанных значений числовых признаков Х и У:

 (х₁ ;y₁),  (х₂ ;y₂), ..., (х_i ;y_i), …, (х_n ;y_n)  .  

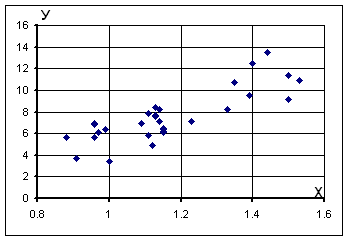Корреляционное поле – это графическое представление статистических данных в прямоугольной системе координат ХОУ, где каждой паре на плоскости соответствует точка. Построенное корреляционное поле позволяет на начальном этапе исследования сделать предварительный вывод как о наличии зависимости между признаками Х и У, так о виде этой зависимости.

5.2 Эмпирическая ломаная регрессии

          Эмпирическая ломаная регрессии строится по точка,  где  х_j – середины интервалов разбиения признака Х;  – средние групповые значения признака У в каждом интервале признака Х:   = (Σ y_i)/n_j . Здесь суммирование ведется только по тем значениям y_i , для которых значение х_i попало в j-тый интервал; n_j – берется из интервального статистического ряда  признака Х для j-го интервала.

5.3 Эмпирический коэффициент детерминации и эмпирическое корреляционное отношение

          Для измерения тесноты связи между признаками Х и У применяются эмпирический коэффициент детерминации и эмпирическое корреляционное отношение.

          Эмпирический коэффициент детерминации находится по формуле:

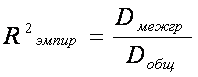 , где D_межгр – межгрупповая дисперсия результативного признака У; D_общ – общая дисперсия результативного признака У ( можно использовать выборочную дисперсию признака У, найденную при одномерном анализе).

Можно также дисперсии определять по формулам:

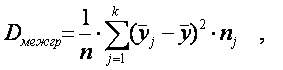                                                 (1)

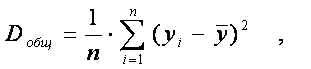                                           (2)

где k – число групп по факторному признаку Х;

n – объем выборки;

y_i – индивидуальные значения результативного признака У;