Математическая статистика в горно-геологических расчетах, страница 29

– его средние групповые значения;

 – среднее значение признака У;

n_j – частота в j – той группе (берется из статистического рядя признака Х).

          Эмпирическое корреляционное отношение равно корню квадратному из коэффициента детерминации

                

5.4 Линейная регрессия

а) Уравнение линейной регрессии с угловым коэффициентом

Уравнение линейной регрессии У на Х имеет вид: 

                        ,                                                (3)

где k –  коэффициент регрессии, b – свободный член уравнения регрессии. Параметры уравнения регрессии определяются по фактическим данным, которые представляют собой набор n пар

 (х_i ;y_i), при помощи метода наименьших квадратов (МНК).

Расчетные формулы имеют вид:

   ,

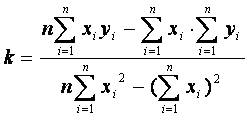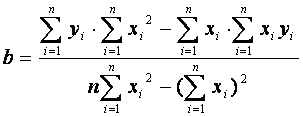   .                              (4)

Если учесть формулы средних и дисперсии признаков Х и У, то расчет можно вести по следующим формулам:

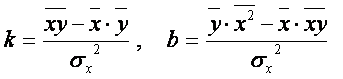  ,                         (5)

где

 

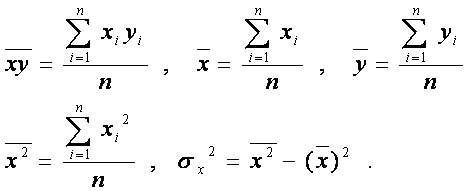
Замечание 1.  Для проверки правильности расчетов можно использовать тождество: 

Замечание 2.   В формулах (5) можно использовать выборочные средние и дисперсии, найденные ранее на этапе одномерного анализа признаков, хотя с учетом группировки может получиться менее точный результат (хотя и более быстрый).

          Расчет сумм, представленных в формулах, удобно производить при помощи табличного процессора Excel, который является электронной версией таблиц. Для расчета в Excel необходимо организовать расчетную таблицу. Ее вид в компьютере будет следующий (для примера взята выборка объемом n = 5):

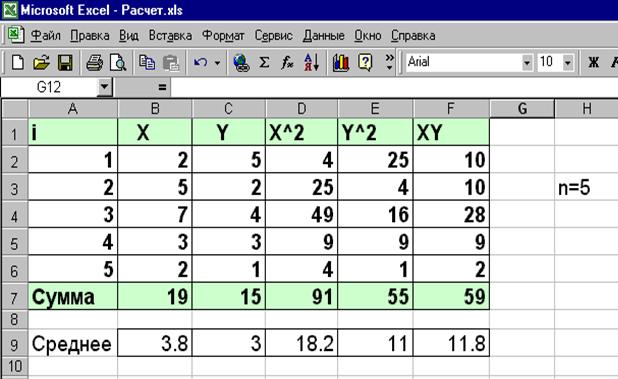
б) Выборочное  линейное уравнение регрессии

Выборочное  линейное уравнение регрессии У на Х имеет вид: 

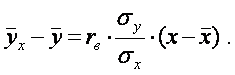                                                 (6)

Выборочное  линейное уравнение регрессии Х на У имеет вид: 

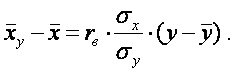                                                           (7)

В этих уравнениях используются следующие формулы:

дисперсия признака Х;

дисперсия признака У;

r_в –  выборочный коэффициент корреляции, вычисляемый по формуле:

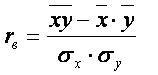                .                                                                  (6)

Если параметры уравнения были рассчитаны по уравнению регрессии с угловым коэффициентом, то выборочный коэффициент корреляции вычисляется по формуле: 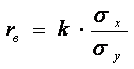                      (7)

5.5 Проверка коэффициента корреляции на значимость.

Пусть признаки Х и У распределены нормально. Из генеральной совокупности извлечена выборка объема n и по ней найден выборочный коэффициент корреляции r_в . Требуется проверить гипотезу о значимости генерального коэффициента корреляции r_г .

Выдвигаются гипотезы

  Основная гипотеза              Н₀ : r_г = 0

  Конкурирующая гипотеза    Н₁ : r_г ≠ 0

 Для проверки гипотезы H ₀  вычисляется наблюдаемое значение критерия: