Математическая статистика в горно-геологических расчетах, страница 22

Требуется при заданном уровне значимости a проверить, подчиняется ли генеральная совокупность выбранному теоретическому закону распределения f(x).

Выдвинем гипотезы

     Н₀:  Признак Х подчиняется закону распределения f(x)                 

    Н₁:  Признак Х не подчиняется закону распределения f(x)

Для проверки сформулированных  гипотез при помощи критерия Колмогорова-Смирнова необходимо выполнить ряд расчетов.

а) Определяют по выборке параметры выбранного теоретического распределения f(x).  Пусть r - число параметров распределения. 

б) Для каждого интервала Х определяют вероятности попадания признака Х в данный интервал. Для этого нужно использовать формулу из теории вероятности

 .

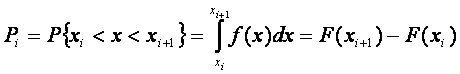Здесь f(x) – дифференциальная функция распределения, F(x) – интегральная функция распределения. Для многих видов распределения имеются таблицы значений f(x) и F(x).

в) Определяют теоретические частоты

                         .

г) Находят накопленные частоты: для эмпирических частот – n×F_n(x) ; для теоретических частот – n×F(x). Для этого следует для каждого интервала последовательно складывать частоты, начиная с первого интервала и заканчивая текущим интервалом. Результаты расчетов удобно записать в таблицу.

д) Далее вычисляют модуль разности накопленных частот в каждом интервале  ôn×F_n(x) – n×F(x)ô = n×ôF_n(x) – ×F(x)ô.

е) Находят наибольший из полученных модулей

  n ×D = max{n×ôF_n(x) – ×F(x)ô}.

 ж) Определяют наблюдаемое значение критерия согласия Колмогорова

                        .                            

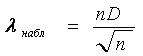Этот критерий является случайной величиной, которая подчиняется закону распределения  Колмогорова.

з) По таблице критических точек (приложение 8), используя заданный уровень значимости a находят критическое значение критерия       l_кр =  l(a).

е) Если в результате сравнения окажется l_набл < l_кр, то нет оснований отвергнуть нулевую гипотезу H₀; если же  l_набл > l_кр, то нулевая гипотеза H₀ отвергается; принимается гипотеза H₁.

Замечание: в критерии Колмогорова рекомендуется брать более “жесткий” уровень значимости  a ³ 0,1. 

4.6  Примеры

Пример 1.

Предполагается, что применение новой технологии в разработке пластовых месторождений  приведет к увеличению качества угля. Результаты контроля по качеству  добытого угля двумя бригадами, работающими в аналогичных условиях, но использующими разные технологии, приведены ниже. Замеры велись по проценту засорения угля, вырабатываемого одной бригадой за смену по старой технологии (признак Х₁) и новой технологии (признак Х₂).

Х₁ (в %): 13; 10,5; 11; 12; 20; 18,8; 10

 Х₂ (в %): 6; 13; 21; 7; 9; 9; 5; 10

Подтверждают ли эти результаты предположение об эффективности применения новой технологии?  Принять a = 0,01 .

Предположить, что выборки получены из нормально распределенных генеральных совокупностей. 

Проведем первичную обработку статистических данных, используя формулы для несгруппированного ряда данных (раздел 2.2, случай а).

Получим по признаку Х₁ :  объем выборки  n=7; 

Выборочная средняя  (13+10,5+11+12+20+18,8+10)/7= 13,61

(13²+10,5²+11²+12²+20²+18,8²+10²)/7= 199,67

Выборочная дисперсия D_в = 199,67 –13,61² = 14,44