Математическая статистика в горно-геологических расчетах, страница 24

.

Здесь используются нормированная нормальная случайная величина   .  Функция Лапласа Ф(z )вычисляется по таблице (приложение 2). При этом учитываем, что

   Ф(–z) = – Ф(z);    Ф(– ¥) = –0,5 ;   Ф(+ ¥) = 0,5 .

В данном случае вместо случайной величины Х  берем случайную величину У.   Далее  заполним таблицу по формулам:    ;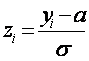  

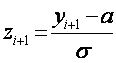
причем крайнюю левую точку интервала заменяем на  – ¥ ; крайнюю правую точку заменяем на + ¥, поскольку теоретическое нормальное распределение определено на всей числовой оси.

Теоретические частоты найдем по формуле:

где функция Лапласа Ф(z)вычисляется по таблице (приложение 2). При этом учитываем, что     Ф(–z) = – Ф(z);    Ф(– ¥) = –0,5 ;   Ф(+ ¥) = 0,5 .

Получим таблицу: