Математическая статистика в горно-геологических расчетах, страница 27

Условный нуль : С=600.

Проверка: 74 = 122 + 2·(–44) + 40  –  верно.

Из таблицы находим условные моменты:

М₁ =  -44/40 = –1,1;   М₂ = 122/40 = 3,05.

Выборочная средняя равна:

 =М₁·h +C =  380.

Выборочная дисперсия равна:

D_в = [M₂  - (M₁)²]·h²  =  73600          

Выборочное среднее квадратическое отклонение равно

271,2932 .

S ² =  ;

 .

Полученные результаты позволяют сделать следующие выводы.

Среднее время безотказной работы путевого стопора по выборке равно 380 час. Средний разброс времени безотказной работы путевого стопора вокруг среднего  по выборке равен 274,749 час.

Проверим гипотезу о показательном законе распределения распределении признака Х.  Используем критерий Колмогорова –Смирнова.

Показательный закон распределения является однопараметрическим распределением с параметром l.  Оценим параметр l с помощью характеристик выборки  следующим образом

l   .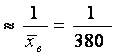

Для каждого интервала признака Х необходимо вычислить вероятности попадания признака  в данный интервал. Используем готовую формулу из теории вероятности для величины, имеющей показательное распределение:

.

Далее  заполним таблицу, причем крайнюю левую точку интервала заменяем на 0 ; крайнюю правую точку заменяем на + ¥, поскольку теоретическое показательное распределение определено для положительных значений аргумента.

Теоретические частоты найдем по формуле:

 ,       n=40 .

Находим накопленные частоты: для эмпирических частот – n×F_n(x) ; для теоретических частот – n×F(x).  Для этого следует для каждого интервала последовательно складываем частоты, начиная с первого интервала и заканчивая текущим интервалом. Затем вычисляем модуль разности накопленных частот в каждом интервале ôn×F_n(x) – n×F(x)ô = n×ôF_n(x) – ×F(x)ô. Заполним таблицу.