Математическая статистика в горно-геологических расчетах, страница 4

·  по статистическому ряду при одномерном анализе;

·  по закону распределения при одномерном анализе.

Для проверки по корреляционному полю  случайных величин Х и У, не разбитых на дискретные категории,  необходимо построить точки в прямоугольной системе координат   (х₁ ;y₁),  (х₂ ;y₂), ..., (х_i ;y_i), …, (х_n ;y_n)  .  Полученное поле точек (диаграмма рассеяния) позволяет определить грубые ошибки  и выбросы, не замеченные одномерным анализом каждой из переменных.

Для примера приведем корреляционное поле, где отмечены две точки, которые явно являются ошибочными.

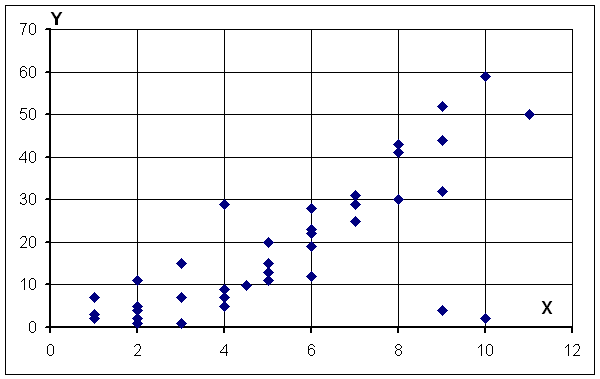
В случаях выявления подобных точек не следует автоматически   исключать их из выборки. Сначала надо проанализировать ситуацию, выявить возможные пути ошибок в каждом конкретном случае, а затем принимать решение по исключению данных из выборки. Если таких точек будет много, то, возможно, их надо выделить в отдельную группу.

В некоторых случаях с помощью корреляционного поля можно выявить не только аномальности в числовых данных, но и установить некоторые закономерности.

Возьмем такой пример. Пусть требуется установить, как мощность разрабатываемого пласта влияет на суточную участковую добычу угля. Была взята простая случайная бесповторная выборка по ряду показателей из нескольких шахт. Построено корреляционное поле.

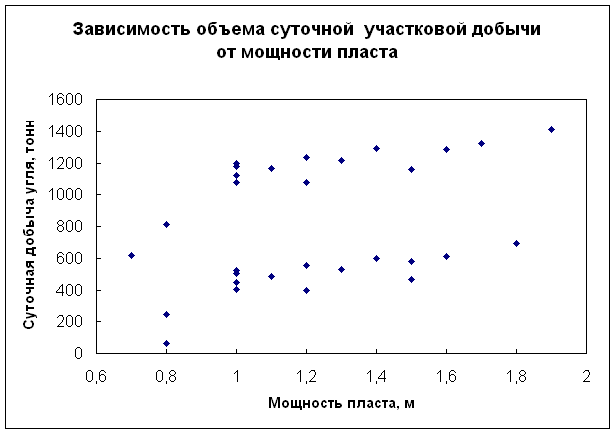
Из данной диаграммы видно, что множество точек корреляционного поля четко распадается на два подмножества (верхнее В и нижнее Н). Последующий анализ данных с учетом других, в том числе и качественных признаков, выявил, что множество Н соответствует выбросоопасным пластам угля, а множество В – не выбросоопасным пластам. Поэтому, на данном этапе исследования целесообразно проводить обработку статистических данных отдельно для  выбросоопасных и не выбросоопасных пластов.

1.2 Группировка статистических данных

Первичная обработка статистических данных позволяет получить из исходного материала путем группировки статистический ряд (точечный или интервальный), а также эмпирическую плотность распределения и эмпирическую  функцию распределения признака Х. Основные этапы первичной обработки:

а) определение минимального (х_min)  и максимального (х_mах) элементов выборки;

б) определение рационального числа интервалов разбиения. Здесь нужно использовать формулу Стэрджесса: 

k = 1 + 3,322× lg n при n <100;   

k £ 10                            при n ³ 100.

в) определение шага интервала   h = (х_max – х_min) / k

    *допускается округлять в удобную для пользователя сторону.

г) подсчет числа частот n_i  (можно при помощи штриховой отметки);

д) заполнение таблицы. Шаблон таблицы приводится ниже.